(内容移動)
前の回に内容を移動して合併し(4+5)としました.
ibaibabaibai-h.hatenablog.com
はしか物語(4+5) 成人麻疹体験記
最後に,麻疹のサイエンスを面白がっていたら,自分が罹ってしまった,というお話.麻疹の発症数はその後急激に減っているので,いまでは珍しい体験ということになるかもしれません.長くなったので前後編に分けます.
初夏6月,謎の病気になる
最初の兆候は筋肉痛だった.いや腰痛だったかもしれない.
体を使った覚えがなかったし,以前にインフルエンザになったときのことを思い出したので,ジムに行く前に体温を測ったら熱があった.これが,謎の病気のはじまりだった.
その後のことは,もう15年も前のことで記憶がはっきりしないが,症状ごとに思い出すことを書いてみる.
熱はいったん下がるかのように思えて,他の症状が出たあとで,また上がった.再度上がったあとも上下が激しく,解熱するときは奇妙な快癒感があって,ふわりふわりと体が浮くような気がする.
厄介なことに季節が6月だった.ずっと以前に夏型過敏性肺炎というカビのアレルギーになったことがあり,その症状(突然の発熱)が始まるのが6月末なのである.転居して以来,症状は出なくなったのだが,咳が出だしたり,目がかゆくなったりした*1こともあり,かなり後までその再発の可能性を疑っていた.
次に発疹.熱が出て寝ているときに,耳の下の皮膚が微妙にかゆくなり,触ってみるとなにか出来ているように思えた.全然大したことはないように思えたので,試しに塗り薬を顔半分だけに塗って,効くかどうか比較してみたりして遊んでいたのだが・・ それがはしかの発疹の出始めだったのだ.
やがて発疹が本格的になって,また新たな心配が起きた.実はその1年半ほど前に大腸検査で腸に口内炎のようなアフタが点在するのが見つかっていた.10年以上もたって,それは難病のクローン病の初期病変だったとわかるのだが,当時は別の難病のベーチェット病を疑っていた.疑ってはいたが,あまり症状が出てこないので,そろそろ違うのじゃないかと思い始めたところだった.
しかし,発熱ととも発疹ができたのでは,アヤシイと思わざるを得ない.ちなみに発疹は手のひらにもできた.「手のひらにもできる発疹」で調べると・・梅毒.いやそれは違うと思うぞ.
はしかの発疹を生検するというのは,あとから考えるとおかしいのだが,本気でベーチェット病などを疑っていたので,皮膚科で切り取って調べた.
先生「ここから取りますか」
私「ううむ,ティピカルなところを取らないといけませんね.ここは?」
先生「いいけど顔だからさ」
・・しまった俺の顔だった!
そして極め付けは口内炎.麻疹の特徴とされるコプリック斑は,どの解説にもあるように,数日で自然に消えてしまうのがふつうである.私の場合は全く普通ではなかった.消えるどころか無数に増えて,歯茎や頬の粘膜を覆いつくしたのだ! これはかなりレアなケースだと思われる.
ベーチェット病を疑っていた私が動転したのも無理はないところである.ただ,なんとなく普通のアフタ性口内炎とは違う気がしていた.最初はあまり痛くなくて,上に粘膜が被っていて,あとから破れるみたいなのだ.アフタ性口内炎は(ベーチェット病の口内炎も同じだと思うが)最初から赤くてさわると激イタで,それから白くなる.
ここまでのまとめ
・症状
熱
鼻水,結膜炎,咳
発疹(耳の下からはじまる)
口内炎(頬の内側,歯茎に多発)
・鑑別
夏型過敏性肺炎
ベーチェット病
なんらかのウィルス感染症
行った病院は,ベーチェット疑いで受診していた大学病院のリウマチ・膠原病科と,そこから紹介された同じ病院の皮膚科.ほかにかかりつけの耳鼻科にも相談した.
耳鼻科の先生はウィルス感染症を疑っていくつか抗体検査をしたが,そこには麻疹は含まれていなかった.皮膚科の先生は当然疑ったらしいが,後頭部のリンパ節が腫れていないことで,違うのでは,と思ったようだ(だいぶ後になって画鋲を頭にねじ込んだように硬く腫れて痛んだ).私もネットで「コプリック班」を検索するまでは行ったが,そこまでだった.母親は「はしか」というのが頭をかすめたが,怒られると思って黙っていた.と後で言った.みんなで,はしかのまわりをぐるぐる回っていたように思える.
お見事
無数の口内炎でたまげたので,膠原病内科の先生に再度受診した.診察日でなかったと思うが,外来に出てきて下さって嬉しかった.
さっそく「先生エライことです」といって口を開けてみせると,しばらく眺めて「これは違いますね.ベーチェットではありません」 ・・なんでわかるのかというと,ふつうのアフタ性口内炎やベーチェットの口内炎は2個が接近すると合体して融合する.ところが私のは融合していない.なるほど~~
ちょっと安心したが,まだ病名はわからない.もう一度皮膚科で診てもらうのがよいだろうということで,先生が親切に電話をかけてくれた.
まだ残っている皮膚科の若い先生が診てくださるとのことで,皮膚科に移動.
皮膚科の先生「えーと,これから私がイチから虚心に質問しますから答えてください」
おおお,何かシャーロックホームズみたいになってきたぞ.
質問が始まって,一所懸命に答える私.
ようやく終わって,先生
「あなたは麻疹にかかっている可能性が高いです」
・・おもわず「お見事」と小さく呟いてしまった.
こうして,ようやく診断はついたが,この後に大変なことが待っていたのだ.
入院
あとで聞いてみると,その年は麻疹の当たり年で,皮膚科病棟にはすでに麻疹患者がたくさん入院していたという話である.そうすると,さっきのシャーロックホームズは実は先生の小芝居で,最初からはしかに決まっていると思っていたとか・・とちょっと考えたが,ともかく正しい診断がついて有り難かった.
成人麻疹だしウロウロして人に伝染させるのも何だというので,入院決定.そのころはまだ父母がいたので「家族に電話しに下に行きます」といったら止められてしまった.なんだが「凄い感染力のある伝染病患者だが大抵の人には無害」という謎のポジションの人になってしまった.病室も個室に入ってくれということに.
(注記)これは当時の実感をあらわしたものですが,実際には免疫を持たない人も多く,麻疹が病院の待合室などで簡単にうつるほどの感染力を持っているため,深刻な問題になっています.はしかを心配して病院やクリニックに行くときは,必ず事前に電話連絡をして対処をお願いするようにしてください.もちろん待合室だけでなく,電車やエレベーターでもうつりますし,簡単なマスクでは十分な効果がないようです.
それまでも咳が出ていたが,病室に行く途中で妙に息苦しい「酸素の足りない感じ」がして,「あれっ,これは過敏性肺炎のときに似ている」と思ったが,胸部レントゲンには問題がないとのこと.
困った患者
無事入院して安心 ・・かと思ったが,その晩はつらい状態に.
まず,水下痢.これは麻疹ウイルスが腸に行ったせいだと思われるが,とうとうおむつ状態に.もうひとつ困ったのは,酸素飽和度を測るパルスオキシメータを付けられたのだが,これの警報が夜中鳴るのである.看護師さんが毎回来て止めるのだが,そんなには心配していないようだ.低酸素血症で警報って,ヤバくないのか?
それで,朝になって「呼吸器内科を呼んでくれ」「CTを撮ってくれ」と叫ぶのだが,反応が芳しくない.ここが正念場と思って,再三要求すると「呼吸器を呼ぶならまず(動脈血酸素分圧をはかるために)動脈血を取らないと」と.
思わず(皮膚科で動脈の採血とか滅多にないよな?大丈夫か?)と思ったが,勢いがついているので「いいですよ」と言ってしまう.言ってから後悔したが,実際には手際よく麻酔して腕の動脈を刺して,何の問題もなかった.
しばらくして,呼吸器内科医が来たが,胸の音だけ聴いて,問題なさそうだし,CTを撮る必要はないとの由.
病室の入り口から覗くと,先生は帰りにナースステーションに寄って何やら話している.困った患者だということになったのかなあ.
騒いで正解だったらしい
ところが,しばらくして看護師さんが来て「CTを撮るので来てください」と.あれれ?
車いすでなるべく人の近くによらないようにしてCTの部屋へ.当時はまだ2cmとかの厚めのスライスで,息とめもけっこう大変だった.
部屋に戻ってしばらくすると,皮膚科の担当の先生が説明に来た.
実は,呼吸器の先生が来たときは,まだ動脈血酸素の結果は出ていなかった.結果が出たら,異常に低い値なので,急きょ方針を変更してCTを撮影した.CTのイメージでは2cmのスライス1枚だけに,白い影が見えた.肺炎の初期像の可能性がある.
それだけの影で,低酸素というのは普通ではありえない.「画像に見合わない低酸素血症」ということになる.理由としては,これから画像上にもっと広範囲の変化があらわれる寸前の姿をとらえたということが考えられる.
その後は,いきなり総力戦になった.「厚木も入間も全部上げろ!」という感じだ.
まずは酸素吸入である.次にガンマグロブリンと抗菌剤の点滴.麻疹ウィルスによる肺炎と2次感染による細菌性肺炎の両方の可能性があるが,鑑別している余裕はないので両方同時に対処というわけだ.「セフェム系はアレルギーあるかも」と申告したので,抗菌剤も2剤.合計3種類を順に点滴に入れる.
どうせなら混ぜて全部いっぺんに入れたら?とまた余計なことを聞いてしまったが,これは素人考えで,アレルギー反応などが起きたときに困る.それでも急ぐために2+1に分けて落とすことになった.
ガンマグロブリンは血液製剤なので,万一のために製造番号を聞いて,その控えはいまでもどこかにある.
この日だったか,次の日だったか,夜に主任の先生が回ってきて,いろいろ慰めてくれてありがたかった.
あとは順調に回復
そのあとは,とりたてて何も起こらず,順調に回復して,1週間前後で退院となった.
肺炎がわかってから説明に来た先生が「麻疹肺炎の死亡率は文献によると2%から70%です」(正確な数字は忘れたが,確かそのくらいの幅があった)と大真面目で言うので困った.当時はエビデンスということが言われはじめたばかりだったので,説明の仕方も慣れていなかったのだろう.見舞いに来た友達にそれをそのまま言ったところ,なぜか高いほうの数字だけが伝わって,えらく心配されたのを覚えている.
この病院の個室はメニューが違って,かなり豪華な献立だということを知った.よその病院でどうかは知らない.その後クローン病で別の病院の個室にしたこともあるが,どっちにしても,その病名ではトンカツとかを食べるわけにはいかない.
短い入院だったが,一夜,隣の部屋の患者が危篤になって,家族が深夜に詰めかけて,とうとうなくなった.びっくりしたが,その頃はもうだいぶん治っていたこともあり,さほど自分の身に引き寄せて考えることはなかった.40歳で父母が存命だと死はまだまだ遠い世界だ..
皮膚科は女性医師の割合が多い.チームで入院患者を診るというシステムだったが,リーダーの先生だけ男性で,ほかの数人は女性だった.回診は華やかな感じで,皮膚科に入院した特典のような気がした
回診のたびに,先生たちが,酸素飽和度でなく,酸素分圧で話をするので困った.しょうがないので,頭の中で線形の補間式を作って換算しようと試みたが,さっぱりわからなかった.家に帰って調べると,酸素飽和度と酸素分圧は直線関係にないことを知った.生物の勉強はしておくべきものである.
麻疹に罹ると自己免疫疾患がよくなることがある?
これで体験記は終わりだが,ちょっと余談.
前にも書いたように,麻疹ウィルスは感染した人のリンパ球や関連した臓器に感染し,免疫系をひどく破壊する.これは,潜伏している結核などの疾患を再活性化させることもある一方で,免疫系が暴走して自分の体を傷つけている場合には,病気をよくする可能性があるかもしれない.
原論文は確認していないが,「腎臓の病気であるネフローゼ症候群が,麻疹に罹ったあとでしばしば軽快する」という話がウェブのあちこちに載っている.「大昔には意図的にそれを使ったネフローゼの治療法が提案されたことがある」というのも,どこかで読んだ記憶がある.
クローン病はどうだろう.成人麻疹になる何年も前から腹具合が悪くなることがあったが,その1年半くらい前に腸にアフタが多発していることが発見された.しかし,そのあと何年も悪化することはなく,それから10年以上もたって,特定疾患のクローン病であると診断された.とても進行が遅かったような気がするが,もしかして,成人麻疹になったのが「効いた」ということはないだろうか.
クローン病では免疫調節薬を使ってTリンパ球の減少を狙った治療が行われる.また,レミケードなどの抗TNF抗体も,Tリンパ球の破壊を通じて効果を表わすと考えられている.そう考えると,因果関係の立証は無理としても,麻疹が荒療治になったのでは,という気もしないではない.2度はできない「治療」なのだが.
もうひとつ
もうひとつおまけ.
退院後に,顔の皮膚の生検の結果を聞きに行った,
すると,先生が怪訝な顔をして,検体から微小な肉芽腫が検出されたが,はしかでそういう話は文献にもないし・・と言われた.
反射的に「検体の取り違えってことはないですよね」といったら,先生は椅子から飛び上がったが,同じ日に似た検査をした人はいないことがわかった.
肉芽腫といえばクローン病に特徴的な症状である.腸のアフタはクローン病の可能性もあると知っていたので「もしや俺の顔はクローン病」と一瞬考えたが,すぐに「ないない」と打ち消した.
ずっとたってクローン病と診断されて,それを思い出した.もし,あれがクローン病がらみであれば,一般に,クローン病患者の見た目健康な皮膚を生検すると肉芽腫が出たりするのではなかろうか*2.何となく気になっている.
はしか物語(3)【改訂版】 当たり年・外れ年・カオス
最初に戻って,麻疹の流行を非線形力学系の視点から眺める.ここに書いたようなことはいろいろな伝染病にあてはまる可能性があるが,(1)感染力が強く,(2)感染して症状の出ない人がほとんどおらず,(3)多くの人が比較的すみやかに回復し,(4)回復後は相当の期間にわたって強い免疫が保たれる,といった性質が,麻疹を特に興味深いものにしている.
麻疹のダイナミクス再び
最初の回では患者の数の変動をあらわす確率モデルの例を考えた.伝染病が「自滅」しては再生する様子を示すにはよいが,実際の麻疹のモデルと考えると,いろいろ問題がある.
まず,ロンドンのような大きな都市では,麻疹は毎年流行するので,流行の周期は1年に固定されていることになる.大きい都市での変動は,最初の回で青い線で書いたグラフに相当するが,モデルでは流行の周期は都市の大きさ(あるいは新しく出生して入れ替わる数)によって連続的に変わるので,明らかに事実とは合っていない.
実際には,大きな都市で周期的な流行を作るのは,さまざまなパラメータの季節変動だと考えられる.特に新入学などによる「患者からまだ感染していない人への伝達効率」の季節変動が重要だとされる.あとで紹介するモデルでも,この部分に季節変動を入れている.
一方,最初の回で赤い線で書いたグラフに相当するのはもっと小さい都市である.この場合には,絶滅と再侵入によって周期的な流行が起きる.実際の麻疹でも,小さな都市での流行の周期は都市のサイズによって変化することが知られており,その意味ではいまの確率モデルはかなりいい線をいっている.バートレットなどの確率モデルの研究は主にこちらの場合を想定していると思われる.
最初の回に紹介した文献に実際の麻疹の時系列データがいくつか出ているので紹介しておく.
こちらのリンクから読める英文文献のFig.1には,London(300万人),Plymouth(21万人),Teignmouth(1万人)の各都市での1940年代から1960年代の麻疹の流行が示されている.この3つはそれぞれ,(1) ほぼ毎年流行し非流行期にも患者数がゼロにはならない (2) ほぼ毎年流行するが非流行期には患者数がゼロになる (3) 独自の周期でやや不規則に流行する,の典型例とされる(ゼロになるかどうかは地図上のどの範囲をユニットとして考えるかにもよるように思えるが)
A stochastic model for extinction and recurrence of epidemics: estimation and inference for measles outbreaks
日本語のこれ(PDF) の図5(ワクチンが無い時代の麻疹の流行周期)には都市や島の人口による周期の変化を示すデータが出ている.大きな都市ほど周期が短いことがわかる.
http://www.eiken.co.jp/modern_media/backnumber/pdf/MM1007_03.pdf
最初の回に紹介したモデルは,それ以外にも問題がある.実は,確率的要素のないモデル(この回の最後に出てくる微分方程式モデル)は季節変動を組み込まないと振動がしだいに減衰して安定点に収束してしまうのである.最初の回のモデルで突然の絶滅まで振動が続くのは,乱数を入れているため以外に,時間を離散化したためである可能性もある.この場合,ある種の生態学のモデルなどでは,離散時間のモデル(世代の重なりのないモデル)が現実的な場合もあるが,麻疹ではちょっと疑問である.
当たり年と外れ年
以下では,大きな都市での流行について考える.季節変動を取り入れたモデルを作ること自体は難しくないが,単に新入学とか休み明けの影響で流行が決まって,それで1年周期になっている,というのはあまり面白くないように思われる.この場合には,最初の回で見たような,麻疹自体がもつ「振動する性質」は全然出てこないのだろうか.
実は面白いことがある.毎年流行するといっても,実際のデータをよく見ると当たり年と外れ年がおおむね交互にある.つまり2年周期である.
これを論じた論文としてよく引用されるのは
である(フリーで落とせる).Robert Mayはカオスの研究で有名だが,この論文にはカオスは出てこない.オタフク風邪や百日咳では3年周期が見られるとも書いてある.
直観的にいうと,感染のしやすさなどの季節変動が僅かであれば,それに直接に対応して1年周期で患者数や免疫を持つ人の数が増減するだけである.
ところが,もっと季節変動が大きくなると話が違ってくる.たとえば,春先だけ感染のしやすさが増えるとすると,春だけ大量の患者が出て,免疫を持つ人の数もそこでどかっと増える.すると翌年にまで影響が及んで,翌年の春には患者がそれほど発生しない.すると,その次の年にはまたどかっと発生し・・のようになるわけだ.
外部からの駆動による周期のほかに,その整数倍の周期があらわれることがあるのは,一般に「非線形」のシステムの特徴である.おまけ1でちょっとだけ一般論を説明したので,興味のある方は読んでみてほしい.ナトリウム灯の例はちょっと面白いかもしれない.
麻疹のシミュレーション(周期外力あり/乱数なし)
上では2年周期の原因を言葉で説明したが,実際にそうなるかは,そんなに簡単に断言できない.できれば,ちゃんとした数式で2年周期が出したい.
数式としてはいろいろ考えられるが,ここでは以下の論文のものを取り上げよう(麻疹の微分方程式モデル自体は1920年代のSoperとか,さらに前のHamerとかに遡る).
具体的な数式とその解説はおまけ2に書いた.以下では,RのパッケージdeSolveを使って【上のモデル+麻疹用のパラメータ】を解いた結果を見せる(コードはおまけ3を参照).
まず,季節変動の強さをあらわすパラメータの値が0.05の場合.これは純粋の1年周期である.
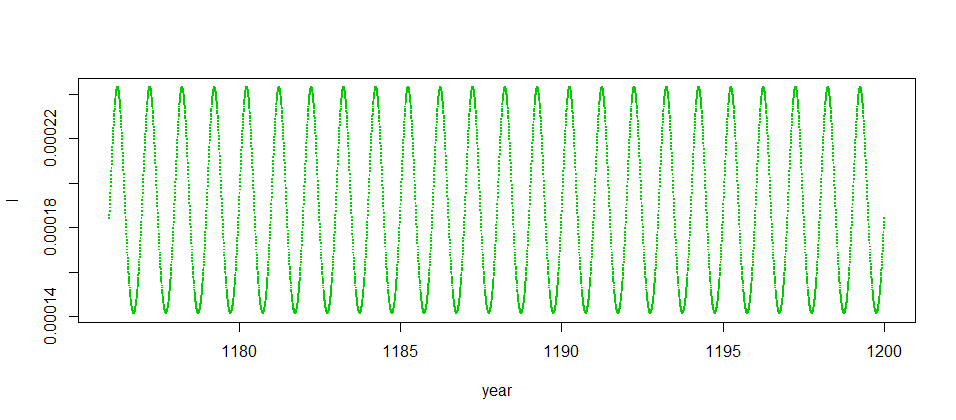
同じモデルでの値を0.2に増やすと当たり年・外れ年のある2年周期に変化する.どちらも最初の過渡的な部分を捨てていることに注意.
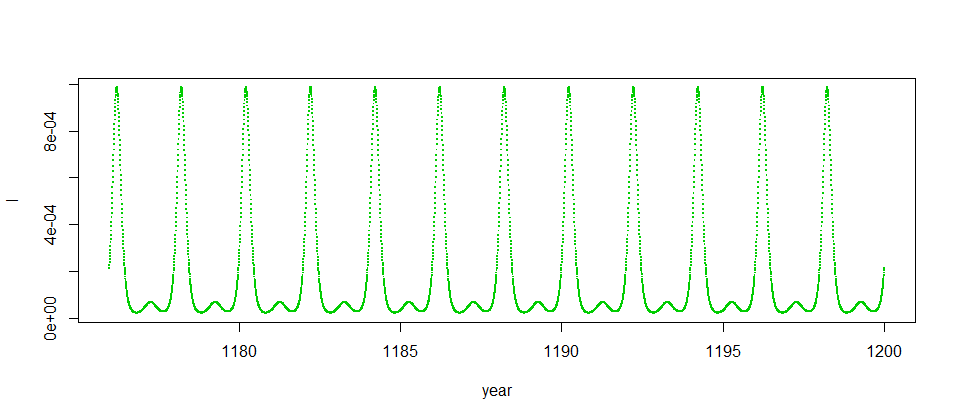
とりあえず,当たり年・外れ年の交代をシミュレートすることができた.
これまであげた文献のほか,LondonとYorkの1973年の論文がデータ解析とシミュレーションの両方でよく知られているらしい.読んでいないが,メモとしてリンクしておく(PDF).
http://yorke.umd.edu/Yorke_papers_most_cited_and_post2000/1973_03_London_I_AMJEpi.pdf
http://yorke.umd.edu/Yorke_papers_most_cited_and_post2000/1973_04_London_II_AMJEpi.pdf
上のほうにあるデータだとオタフク風邪や水疱瘡では,1年以上の周期ははっきりしないようだ.
それ以外の周期も出る
ところが,このモデルは,2年周期だけでなく,他にもいろいろな挙動を示す.
たとえばとすると,1年の整数倍でないような振動が見られる.実はこれは文献に載ってないので,計算ミスと思ったのだが,たぶん正しいようだ(読者が再現できたらツイッターなどで教えてほしい).
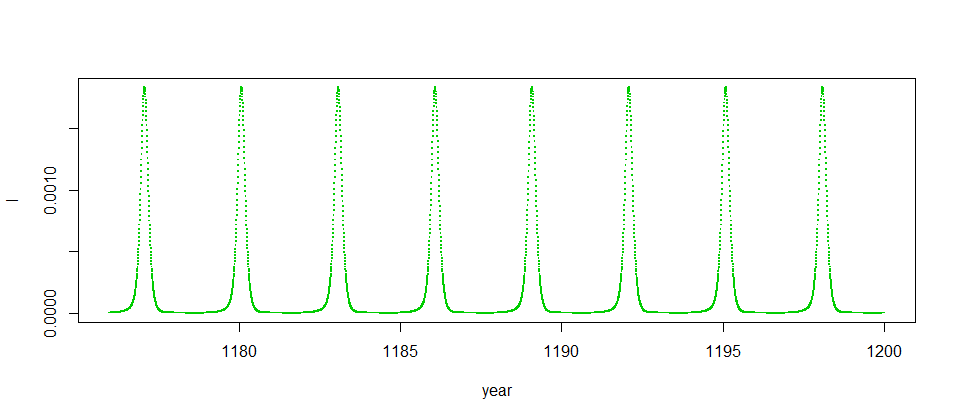
また,季節変動をあらわすパラメータを大きくして行くと,4年周期,8年周期,16年周期・・も出現する.たとえば,8年周期の例はこうなる().
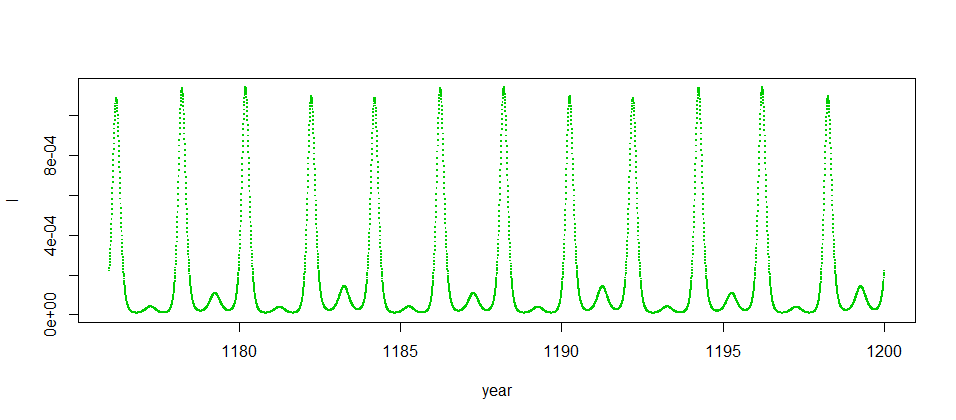
2年周期がベースにあって,丁寧にみると8年周期になっているという感じだ.
カオスも出る
だんだん長い周期が出てきて,最後はどうなってしまうのか? 実はある限界があって,その先は周期解でなく不規則な変化をするようになる.いわゆるカオス解の出現である.
「カオス」については,名前を聞いたことがある人も多いと思う.たまに柑橘類の「カボス」と間違っている人もいるが,そっちではなくて,初期値の僅かな差や微妙な雑音,数値的な丸め誤差で結果が大きくかわる(バタフライ効果)というアレである.乱数を入れなくても,初期値に微妙に依存して,いつまでもランダムに動き続けるのである.
カオスというと文字通り混沌とした状態を想像する人もいると思うが,そういうものばかりではない.メインの変動はほぼ2年周期であって,よく見るとその上に不規則な動きが乗っかっているという場合もある().見かけ上,さっきの8周期とほとんど変わらないが,こんどはいくら長くやっていても周期がない.
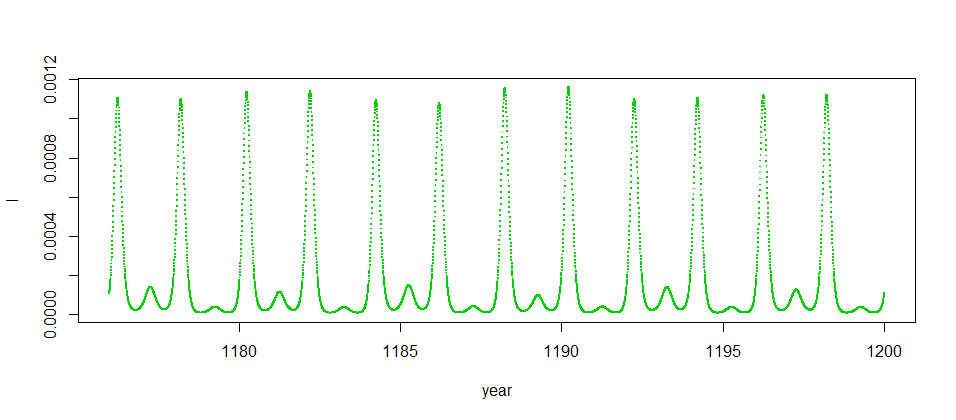
一方で,これはかなりデタラメ感がある().
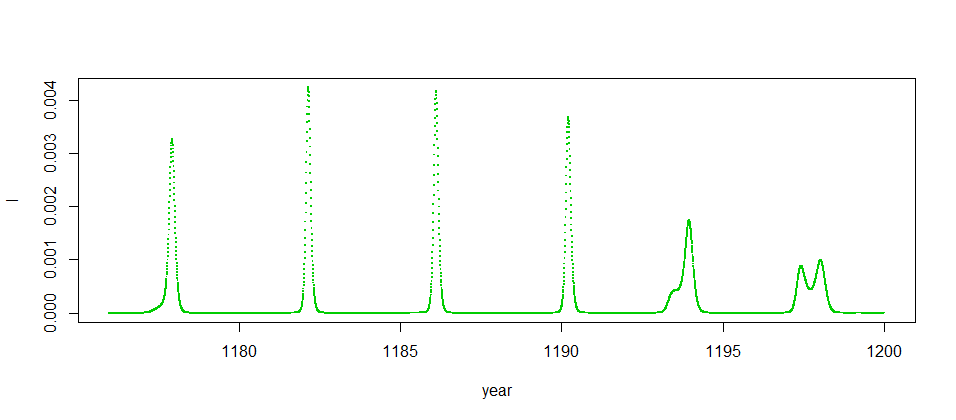
もっと長くプロットすると
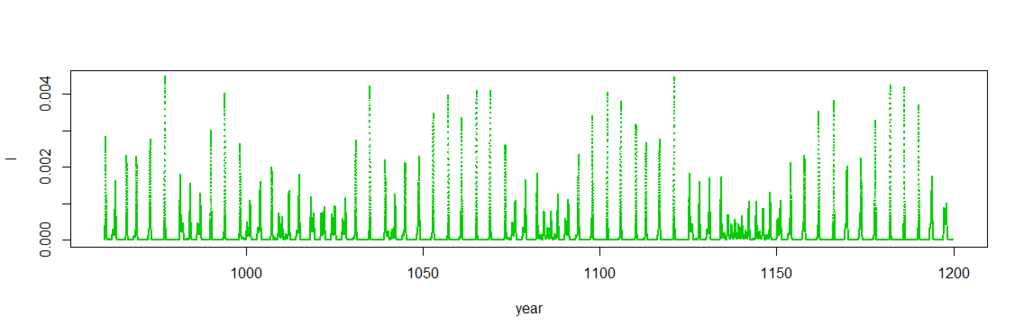
ところが,これには問題があって,Matlabで計算したり,方程式を解くときのやり方(刻み幅)を変えると,結果が変わってしまったりする.それで,最初はプログラムが間違っていると思った.実は解き方だけでなく,の値をホンの僅か変えても違う結果になるので,これは普通でいう間違いというよりはカオス系特有の不安定な振る舞いなのだろう.
基本的には,(1)2年周期がほぼ保たれて僅かに乱れるカオス,(2)2年周期が完全に壊れたカオス,あるいは壊れた状態と2年周期がほぼ保たれた状態を間欠的に移動する,のふたつがあって,ちょっとした計算法やパラメータの違いで入れ替わるように見える.ただし(2)がホンモノであることは十分に確認できていない.
麻疹の時系列はカオスか?
ここで,はっと思いついて実際のデータを見ると,いままで雑音というか外部的なランダムネスのように思えた部分が,(ほぼ2年周期の解が少し不規則になった)カオスなのではないかと思えてくる.
「見た目の通りの大きさの雑音が入っている」と思っていた部分は,「微小な雑音がシステムの性質によって拡大して生じた」ものなのかもしれないのだ.
80年代にさまざまな分野の研究者を襲った「カオス病」の発症である.しかし,実際のデータがカオス解なのか,単に安定な周期解(リミット・サイクル)に雑音が乗ったものを見ているのか,見分けるのは簡単ではない.
実際の麻疹と水疱瘡の時系列データをいろいろな技術を駆使して調べた結果が下の論文にあるが,これによると,水疱瘡の時系列は周期解+外部雑音だが,麻疹はおそらくカオスである可能性が高いとのこと.
カオスだと実際的に何が違うのかは,本当のところよくわからないのだが,麻疹マニアとしては,何となくうれしい気がするのである.
(おまけ1)線形と非線形
大まかにいうと,関数が線形というのは,入力が
のときの出力が
,
のときの出力が
のとき,
に対する出力
が単純な和
になることを意味する.もし
がただの数字ならこれは正比例とか直線関係ということになる(もともと「線形」の「線」は直線の意味である).実際には入力
や出力はもっと複雑にベクトルだったり,「足し算が定義される何か」だったりする.関数でなく方程式についての「線形」は「2つの解の和がまた解になる」ことである.
一般に,システムに周期的な変化を外から加えたとき,何がおきうるかは「線形」のシステムと「非線形」のシステムで違う.
線形のシステムにある振動数で外からの力を入力すると,そのままの振動数で振動する.「振動数」の代わりにその逆数の「周期」といっても同じである.ただし,外力に反応する強さは,そのシステムの特性による.「システムをちょっと引っぱたいてあとは自然に振動させたときの振動数」(固有振動数)に外力の振動数が近いほど,同じ大きさの外力に対する反応は大きい.これを共鳴とか共振といって,たとえば地震や風による建造物の破壊とか,テレビやラジオのチャンネルの選択とか,いろんなことに関係がある.
正確にいうと,最初のうちは固有振動数の振動が外力による振動に重なってみえることがあるが,「摩擦」のようなものが少しでもあると,固有振動に相当する部分は,外からエネルギーが供給されないのでしだいに消えてしまい,外力の周期の部分だけが残る.また「外力の整数倍の周期があらたにできる」ような現象は起きない.
ここで「共鳴」は知っていても「いつも外力と同じ周期で振動する」というのは改めて意識していない人がいるかも知れない.このわかりやすい例としては「高速道路などで使われる黄色いナトリウム灯で照らされた光景」がある.
前に書いたが,光の色は光の振動数に関係しており,物体の色は物体の中身がそれを照らす光に「共鳴」することで反射・吸収が起きて生じる.ナトリウム灯はほぼ決まった振動数なので,照らされた物体の中身もその振動数で揺れ,その振動数の光を出す.だから,どんな物体も黄色くみえる.さらによく見ると,普段黄色く見えるものは明るく,違う色のものは暗く見えるが,これは共鳴の効果である.
これに対して「非線形」の場合には,入れた外力の2倍,3倍・・の周期の振動が起きることがある.上で述べた麻疹の当たり年,外れ年はまさにその例で,もとの1年周期の上にその2倍の2年周期の成分が(位相の山と谷が合うように)かぶっているのである.
(だいぶ前のバージョンで入っていた違う色の光が出てくる話は「2倍の振動数」(半分の周期)で逆でした.これも非線形性のあらわれではあるのですが,ミスリードの可能性があるので削除しました)
(おまけ2)微分方程式の説明
上の計算に用いたモデルは下記のような微分方程式モデルである.これはいわゆるSEIRモデルの仲間(永久的な免疫を仮定しているので4つの変数のうちのRは除いてある)だが,麻疹の場合にはHamerとかSoperという人たちが早い時期に研究している(SEIRモデルの初出とされる論文が1927, Soperが1929, Hamerの研究はさらに前).
Compartmental models in epidemiology - Wikipedia, the free encyclopedia
「感染症と文明」のSEIRモデル : wrong, rogue and log
以下で,変数は S(未感染の人の数;Suseptible),E(暴露して潜伏期にある人の数;Exposed),I(発症して人にうつせる人の数;Infectious).
ここで,季節変動を係数の部分に入れる.新学期は複数あるし,いきなり階段状に変わりそうなのに,コサインかよ~というツッコミは自分もしたい.
式の意味は,式ごとよりも項ごとに見て行くのがわかりやすいと思う.
- 感染:免疫なし→潜伏状態
- 第1式と第2式
- 上で
の季節変動が
で与えられる.
の単位は年.
- 第1式と第2式
- 発症:潜伏状態→病気の状態
- 第2式
- 第2式
- 治癒:病気の状態→免疫ありの状態
- 第3式
- 第3式
- 出生:免疫なしの人が新しく出てくる
- 第1式
- 第1式
- 死亡:出生の分だけ除去される(病気でも死亡率は増えないと仮定)
- 第1式
,第2式
,第3式
- 第1式
(おまけ3)
改稿にあたって種々ご助言頂いた @ghost_orange様,@KuboBook様,およびS氏に感謝します.
上をR言語のパッケージdeSolveで解くコードを掲載しておくが,以下のリンクの上のほう(およびそのリンク)の内容をそっくり使わせて頂いて,式を入れ替えただけである.
Rパッケージ deSolveを使う
http://d.hatena.ne.jp/teramonagi/20150531/1433042797
場合によっては,数百年以上も最初の部分を捨てないと論文のアトラクタに収束しないようだが,そのあたりの現実の麻疹との対応がイマイチよくわからない.
library(deSolve) #方程式とパラメータを設定 parameters=c(b0=1800,b1=0.2,m=0.02,a=35.84,g=100) SEI=function(t, state, parameters) { with(as.list(c(state, parameters)), { b=b0*(1+b1*cos(2*pi*t)) dS =m*(1-S)-b*S*I dE =b*S*I-(m+a)*E dI =a*E-(m+g)*I list(c(dS,dE,dI)) }) } #初期値と刻みを設定 infected=0.0001 initial=c(S=1-infected, E=0, I=infected) times=seq(0, 1200, 0.005) #解く out <- ode(y = initial, times = times, func = SEI, parms = parameters) #プロットする olen=length(out[,4]) plen=olen*0.02 col=3 windows() plot(log(out[(olen-plen):olen,2]),log(out[(olen-plen):olen,4]),col=col,pch=".",xlab="S",ylab="I",cex=2) windows() plot(out[(olen-plen):olen,1],(out[(olen-plen):olen,4]),col=col,pch=".",xlab="year",ylab="I",cex=2)
(メモ)空間パターン
化学反応や非線形素子のネットワークなどで,渦巻きや進行波などのパターンが生じることが知られている,友人が教えてくれた下記の論文では,提案の解析手法を使うと麻疹などの流行に空間パターン(進行波?)が見いだせるとのこと(詳細未見,友人からの情報).
http://www.nature.com/nature/journal/v414/n6865/full/414716a.html
(内容移動)
直前の回に内容を移動してまとめ(1+2)としました.
ibaibabaibai-h.hatenablog.com
はしか物語(1+2) 病気の振動と絶滅,都市の誕生
今回のシリーズは麻疹(はしか)の話.
修士課程で氷の研究をしたあと,博士課程のはじめくらいに,伝染病のシミュレーションを格子の上で走らせて遊んでいたことがある.和文論文をひとつ書いたのだが,いま読むと何をやっているのかよくわからない内容なので,引用するのはやめておく.セル・オートマトンとかepidemic processとかが流行っていたころで,「物理」のセンスとそうでないものの間でなにか模索していたのだと思う.
それから10年以上たって,自分が成人麻疹に罹ってしまい,危ないところだった.2015年で国内由来のはしかは3年連続でゼロになり「排除宣言」がされた由で,輸入される麻疹はあるにしても,発症数は激減している.いまや成人麻疹は貴重な体験かもしれないので,最後の回はその話を書くことにしよう.
(1+2),3【改訂版】,(4+5)の全3回にまとめ直しました.
振動したり絶滅したり
伝染病の流行には振動がみられることがある.病気がどんどん広がって行くと,いちど罹って回復して免疫を持つ人が増える.あるいは人々が死んでしまって感染できる相手がいなくなる.人間にとっては大きな違いだが,病原体にとってはどっちでも同じことで,火事が燃えるものがなくなって自然に消えるような現象(絶滅,extinction)が起きる.
ここで,新しい人が全然加わらなければ,絶滅しかないわけだが,生まれてきたり転入してくる人が一定以上いれば,復活もありうる.病気が下火になるが,ゼロではない状態がしばらく続くと,その間に感染可能な人の数が増えて,あるところから,また「どーん」と流行するわけである.これを繰り返せば振動になる.もちろん振動しているうちに運悪く絶滅してしまう場合もある.
こう書くと,プログラミング好きの人はさっそくモデルを作って試したくなるだろう.確率モデルの詳細は後で示すとして,とりあえず,結果だけ見せよう.
以下の図の横軸は時間(シミュレーションのステップ数),縦軸はその時点で病気に罹っている人の数(あとのプログラムではx[2])である.3つの図は,同じパラメータで,乱数だけ変えたものに対応する.乱数を使ったモデルなので,他の条件が同じでも偶然によって差が生じる点に注意されたい.
まず,そこそこ振動してから絶滅する例.
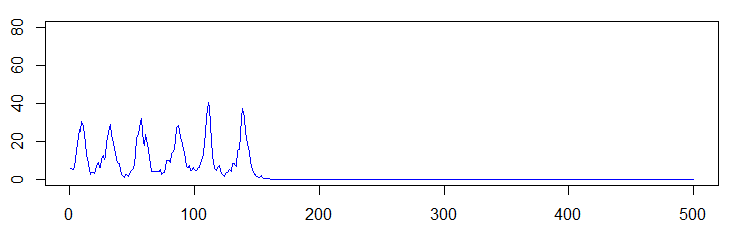
こんどは長持ちの例.
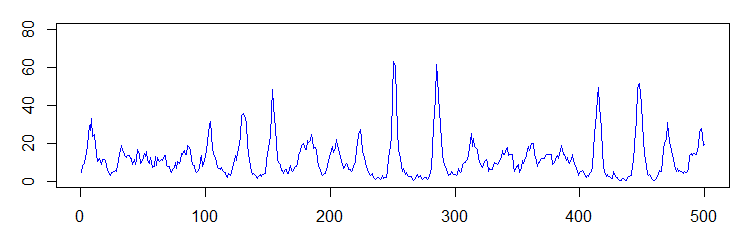
と思うと,広がらずに,あっという間に終わることもある.
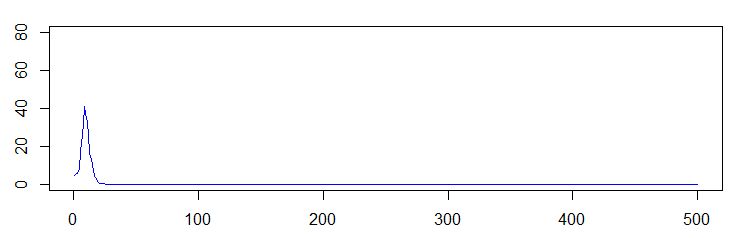
ちょうど微妙なパラメータの値を選んでいるせいもあるが,想像するよりも偶然の余地が大きい.うんと減ってしまったところで,1人でも患者が残っているかどうかで患者数が回復するかどうか決まるわけで,そこで偶然が入るわけである.
Critical Community Size
都市のサイズが小さいと都市内部の出生数が少ないので,すぐに絶滅してしまうが,実際には「外部」があるので,そこからまた病気が侵入する.その結果,見た目は似たような振動が起きるが,よくみると途中で内部の患者がゼロになる期間がある点が違う,
シミュレーションだとこんな感じだ.こんどは「外部」のあるモデルになっているので,絶滅してもいつかは復活できる.ピークが妙に等間隔に見えるのは,絶滅後しばらくは免疫された人が多くて侵入できないためである.刺激されても反応できない「不応期」みたいなものがあるわけだ.
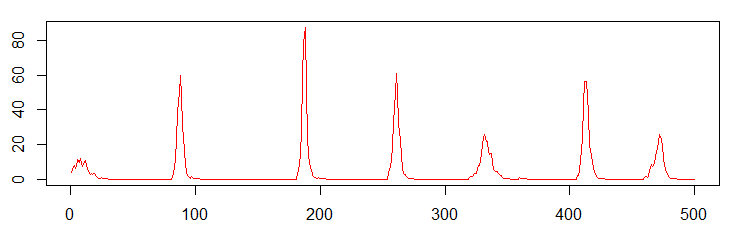
伝染病が維持できる限界の都市のサイズはいろいろなパラメータによって変わるが,これをCritical Community Sizeと呼ぶ.「臨界サイズ」といっても,本当にそこで定性的な性質が変わるわけではなく,目安のようなものである.Critical Community Size以上でも一定の時間内に絶滅する確率は有限だが,非常に小さくなり,実際上はゼロとみなされる.
都市といっても「内と外」がそんなに厳密に分かれているとは限らないので,よりきれいなデータを求めて離島での流行の様子を調べた研究もある(あとの文献参照).小さい島だと外部からの再侵入によって流行が起きるが,大き目の島なら自分の中で病気が維持されることになる.
都市の出現と麻疹のウィルスの進化
いまの話から「人類が都市を形成する以前にはどうだったのだろう」という疑問を思いついた人がいる.
麻疹の場合には Critical Community Size はかなり大きいので,人類のあけぼのの時代には,そんな大きい都市(というか人間が固まって住んでいる場所)はどこにもなかったと考えられる.どこにもないのだから,外部からもらうというわけにもいかないわけで,麻疹ウイルスは自分で自分の首をしめて自滅してしまうほかない.
動物からうつる,と思うかもしれないが,少なくとも現在の麻疹は人間しか罹らない.天然痘と同じで,だからこそワクチンで撲滅しようという話が現実味を持つわけである.
これは麻疹が存在するという事実と矛盾するようであるが,実は,麻疹のウイルスが動物(おそらく牛)から人間に宿主を変えたのはかなり新しく,「都市」が誕生したあとになってからだと考えられている.それまでの間は,麻疹ウィルスはたとえ「種の壁」を超えても,その先ずっと人間の間ではやり続けることはできなかったということになる.
病気にかかるのは個々の人間なのだが,ある意味では「都市」というシステムが病むわけである.
こういう話を聞くと,こんどはウィルスの進化のシミュレーションが作りたくなるが,結局「ウィルスが変異したときに抗原としての重なり(抗体の交差)がどの程度あるのか」といったパラメータの決め方でどういう答えでも出そうで,面白い結果を出すのは難しそうな気がする.
麻疹は猛毒だった?
ところで,麻疹という病気を全く知らない土地にはじめてウイルスが侵入すると,大変な威力を示して,住民の大半が死んでしまう,という話がある.たとえば,フィジー諸島に麻疹が侵入したときは大変に高い死亡率であった伝えられているし,他でもそういう例がある.
「免疫がなかったから」というのは大流行の理由にはなるが,死亡率はまた別の問題である.ひとつ可能性のある説明は,われわれは麻疹に対抗できるように進化したが,麻疹のない土地に住んでいる人たちは抵抗力がないままだった,というものだ.
ここで「進化」と簡単にいったが,その実態は「われわれの先祖のほとんどは麻疹に罹って死んだが,ごく少数のミュータントが恐ろしい病気にも耐えられた.我々はすべてこのミュータントの子孫である」という意味である.
想像してみよう.
猛烈な感染力を示す謎の病気で倒れる人たち.この病気は生体を防御するリンパ球自体を狙って感染し,胸腺などのリンパ組織を破壊してしまうという不気味な性質を持っている.いったん解熱したように見えても,再び熱が上がり,恐ろしい真っ赤な発疹が出て死んでゆく.あっという間にどこもかしこも病人と死体の山となり,人類の希望はついえたかのように思われた.そのとき,ウイルスに打ち勝って回復する特異体質の人がごく少数存在することがわかる.生き延びたミュータントたちが文明を再建したのである.
自分がそういうすごいミュータントの子孫だと思うと,誇らしいような怖ろしいような,ちょっと変な気持ちになる*1,
もっとも,今回改めて調べてみると,これにはほかの可能性もあるようである.グリーンランドにはじめて麻疹が侵入したときは大流行になったが,死亡率はそれほど高くなかったともいう.数十パーセントというような死亡率は,大流行で社会のインフラが崩壊するとか,何かほかの副次的な現象によるのかもしれない.
また,ヨーロッパでは麻疹の死亡率がある時代から下がった,という話もある.この場合は,麻疹ウイルスに対抗できる人間が選択されたというより,ウイルスのほうが変化した,あるいは,栄養状態その他によって人間の生き延びる力が増えた,ということが重要なのかもしれない *2
「都市の発生」には麻疹への耐性が必要だった?
前回紹介した話は「麻疹ウィルスの誕生が都市の形成を前提条件にして可能になった」というものである.
しかし,逆方向の話もありうるのではないか*3.まず,麻疹ウィルスの毒性が(当時の人類に対して相対的に)いまよりずっと強かったと仮定する.また,牛から人間への「種の壁の突破」が比較的容易で,歴史の中で何回も繰り返し起きたとしよう.そういう状況だと,逆に「麻疹に対する抵抗性が進化してはじめて都市というものが可能になった」ということはないだろうか.
また妄想.
古代のどこかの地方で,町が栄えて,都市の原型が形成され,さらに発展して行く.人々は明日の繁栄を疑わないが,少数の古老だけが「こんな賑わいには罰があたる.伝説の赤い悪魔がきっと来る」と不吉な預言をする.・・・ そこでお約束の病気の出現である.無残な赤い発疹.機能しない免疫系.生まれたばかりの都市は無数の墓を残して廃墟になる.人々の記憶こそ毎度曖昧であるが,こうしたことが100年,200年の間隔をおいて繰り返される.バベルの塔の倒壊とは実は麻疹のことだったのだ(嘘).
・・しかし,ついにウィルスに打ち勝つミュータントが赤い悪魔に勝つ日が(さっきの妄想に続く),という筋書きは面白いと思うのだが,やっぱり無理だろうか.
(おまけ)シミュレーション・モデル
シミュレーションのコード
さっきの図を作るのに用いた確率モデルを説明しよう.
いろいろなモデルが考えられるが,以下では離散時間の簡単なモデルを考える*4.また,ここでは「都市」の中にできる感染者の塊(空間パターン)の効果は考えない(いわゆる平均場モデル).「遠くにいる人にはうつらないのではないか」という疑問もあるが,その分はうつりやすさを決めるパラメータ(下記ではlam)の値が小さくなることで表わせるとする.
数式で書くより,時間発展の手続きをプログラムで説明したほうが早そうだ.いつものようにR言語で書くことにすると,コードの全体はこんな感じになる.
xinit=c(75,3) lam=0.01 nu=6 alpha=0.5 theta=0 col=4 k.repeat=1 n.length=500 x.record=array(0,dim=c(n.length,k.repeat)) for (k in c(1:k.repeat)){ x=xinit for (n in c(1:n.length)){ newseed=rpois(1,theta) new=rpois(1,lam*x[1]*(x[2]+newseed)) add=rpois(1,nu) x[1]=x[1]+add-new x[2]=alpha*x[2]+new if(x[1]<0) {print(x);x[1]=0; } if(x[2]<0) {print(x);x[2]=0; } x.record[n,k]=x[2] } } plot(0,0,type="n",xlim=c(1,n.length),ylim=c(0,max(x.record[])),xlab="",ylab="") for(k in c(1:k.repeat)) lines(1:n.length,x.record[,k],col=col)
以下,各ステップを大まかに説明するが,別にこれが標準的なモデルというわけではなく,とりあえずそれらしく動いて遊べるという程度の話である,
モデルのプログラムの説明
各時点でのシステムの状態をきめる変数
x[1] 感染者の数. x[2] 感受性のある人(免疫を持たない人)の数.
x[1]とx[2]を1ステップ時間発展させる手続きは以下の4つで決まる.
1.外部からの感染者の流入
newseed=rpois(1,theta)
ここでは,各時点の外部からの感染者の流入newseedが期待値theta(定数)のポアソン分布に従うと仮定する.rpoisというのはR言語の関数で,期待値を与えてポアソン分布にしたがう乱数を発生させるものである.期待値thetaをゼロにおけば「外部からの感染者の流入なし」のモデルになる.
2.感染
new=rpois(1,lam*x[1]*(x[2]+newseed))
「(内部の感染者数x[2]と外部からの感染者数newseedの和)=感染源の数」と考えて,「感染源の数×感受性のある人の数x[1]」に比例して,新たに起きる感染の数の期待値が定まるとした.それを式で書いたのがlam*x[1]*(x[2]+newseed)である.lamは比例定数.そして,その期待値で定まるポアソン分布で新たな感染者の数newを発生させる*5.
3.回復→免疫獲得(または死亡)
x[2]=alpha*x[2]+new
感染・発病した人は一定割合で回復するとしたのがalpha*x[2]の部分である.alpha=0.5なら各ステップで半分が回復する.それに新たに感染した数newを加えたのが次のx[2]になる.ここは結構アヤシイ*6.なお回復すると「免疫のある人の数」が増えるが,それは計算に直接必要がないので変数にはしていない.
4.出生(または外部からの免疫を持たない人間の流入)
add=rpois(1,nu)
x[1]=x[1]+add-new
期待値nu(定数)のポアソン分布で新しく生まれた人の数addを発生させるのが最初の式.現在のx[1]にaddを加えて,新たに感染した数newを引いたのが次のx[1]になるというのが2番目の式.
かっこわるいけど
このやり方では,離散時間近似のため,差し引いたあとの人数がマイナスになることがあるが,その場合は強引にゼロにしている,
if(x[1]<0) {print(x);x[1]=0; }
if(x[2]<0) {print(x);x[2]=0; }
すべてがポアソン過程と仮定すれば,連続時間のシミュレーションは標準的なテクニックで可能だが,たとえば病気からの回復がポアソン分布で起きるとは思えないので,必ずしもリアルとはいえないだろう.
完全にリアルにするには個人ごとに状態を設定するのが一番だが,10000人いれば10000の個体(エージェント)を動かすシミュレーションをすることになり,なかなか大変である.実際にスパコンや京コンピューターでそうしたモデルを実装している研究もある.
プログラムの説明の補足
- 乱数のseedは指定していないので毎回出る絵が変わる
- 青い線のグラフを描いたパラメータ.
- lam=0.01
- nu=6
- alpha=0.5
- theta=0
- 外部からの流入で感染者が維持されている状態(赤い線のグラフ)では以下を変更.
- nu=2
- theta=0.05
- x[1]とx[2]の初期値 xinit=c(75,3)
- 時系列の長さ n.length=500
- 全体の繰り返し数 k.repeat=1
- プロットの色 col=4
歴史とか文献とか
ウェブで読める以下の解説は麻疹について包括的に扱っていて大変興味深い(PDF)
http://www.eiken.co.jp/modern_media/backnumber/pdf/MM1007_03.pdf
国立感染症研究所の解説(旧ウェブ,やや古い情報)主に病気としての麻疹についてのまとめ.
IDSC 感染症情報センター
確か自分はこの記事を読んで興味を持ったような気がする.島嶼の麻疹流行の話.
クリフ・ハゲット 「はしかはどのように拡がるか」 日経サイエンス1984年7月号
島嶼の麻疹流行については60年代のこの論文が有名.都市についての話もこれがオリジナルではないかと思う.
Measles endemicity in insular populations: Critical community size and its evolutionary implication
Critical Community Sizeについては,バートレットやケンドールといった昔の大御所の50年代の研究がある.この際勉強してみようかと思ったが,確率過程は得意でないのと,ひたすら読みにくいため沈没.いちばんの基本となる「出生死滅過程」については解析的な取り扱いがフェラーの確率論の本にある.
バートレットも解析的な扱いの限界は理解しており,同じマンチェスター大学でやっていた初期の電子計算機プロジェクトでシミュレーションを走らせている.その話は書いていないが,計算機プロジェクトの話はウィキペディアにある.
Manchester computers - Wikipedia, the free encyclopedia
最後に割合新しいフリーアクセスの論文(モデルのパラメータのデータからの推定がメイン)をメモしておく.
A stochastic model for extinction and recurrence of epidemics: estimation and inference for measles outbreaks
*1:まあこれは「すべての人は無数の精子の戦いに勝利して生まれてきた」というのとあんまり変わらないかもしれないが.
*2:この節の執筆にあたっては,「麻疹,フィジー」で検索すると上位でヒットする以下の文書の情報を一部参考にした.https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0ahUKEwjdu9KG-afOAhXHKZQKHYd6CnkQFgg0MAM&url=http%3A%2F%2Fwww.tm.nagasaki-u.ac.jp%2Fnewrect%2Fjapanese%2Finfectious%2581%2595civilization%2Fprologue.doc&usg=AFQjCNEyWHpOCRcJcSj_8ePE3-ldHOAf5w&sig2=-vYXtMO7-lof9iMrRBK8Iw おそらくこのサイトを運営されている方の訳書・著書のいずれかの一部ではないかと思われるが確認できていない. 長崎大学 熱帯医学研究所 国際保健学分野
*3:こちらのほうの話は,自分で思いついたのか,どこかで聞いたのか忘れてしまった.
*4:パラメータや都市サイズは麻疹の現実的な値には合わせていない.また潜伏期は入っていない.
*5:感染者の数についてポアソン分布でなく逆2項分布を勧める文献もある.
*6:文献には1ステップで全部治ってしまうとする(というか,発症から治るまでの時間を1ステップに対応させる)やり方が出ていたので試したが,なぜかそれだとうまく動かなかった(パラメータが悪い?)
岩波データサイエンス3巻 「因果推論」 トークイベントのお知らせ
岩波データサイエンス3巻(DS3)の特集「因果推論」関連のトークイベントのお知らせです.
登録不要・入場無料 6月30日(木) 19:00-21:10(18:45開場)
東大医学部2号館本館大講堂
東京大学 [本郷キャンパスマップ(医学部2号館本館)]
最寄り駅は本郷三丁目(丸の内線)ですが,根津(千代田線)やお茶の水駅から直接歩くこともできます.遅刻の場合はお茶の水でタクシーを捕まえれられれば最速で着きます.2号館に着いたあとの場所は掲示を出す予定です.三四郎池のまわりで工事をしていますが通行に特段の支障はなさそう.
18:45 開場
19:00-19:10 opening 伊庭幸人(統計数理研究所) 10分
19:10-19:25 「因果推論ことはじめ」 立森久照(国立精神・神経医療研究センター) 15分
19:25-19:55 「実社会に役立つ因果効果推定―序論―」 星野崇宏(慶應義塾大学・経済学研究科) 30分
19:55-20:15 休憩 20分
20:15-20:35 津川友介(ハーバード公衆衛生大学院),中村知繁(慶應義塾大学・理工学研究科),加藤諒(慶應義塾大学・経済学研究科),蛯名優子(画家)ほか執筆者・表紙原画作者の紹介 20分
20:35-21:05 「医学研究におけるエビデンス統合の新しい方法」 野間久史(統計数理研究所) 30分
21:05-21:10 closingと岩波ds4のお知らせ 伊庭幸人(統計数理研究所) 5分
内容は「ニコニコ生放送」で生中継されますが,申し訳ないのですが,タイムシフト視聴はできません(事前登録の場合もプレミアム会員の場合も不可です).また配信は技術に詳しい方に依頼していますが,電波状況などでうまくいかない場合もあります.ご不便をおかけしますが,よろしくご理解のほどお願いします.
live.nicovideo.jp
* * *
まだ本を買ってない方や「因果推論って何」という方の参加も大歓迎です.伊庭のイントロと立森さんの話では,そういう方のために,本の内容やテーマについて説明します.
続く講演では,わが国での因果推論研究の第一人者のおひとりであり,岩波DSにも執筆頂いた星野さんにご登壇頂きます.
因果推論の分野は,歴史的に医学や疫学,それに政策決定に関する経済学やほかの社会科学,また心理学,教育学などで発展してきた面もありますが,今回講演される星野さんはビジネスへの応用にも大いに興味を持たれています.そちらの方面に関心のある方はぜひ参加されて直接質問をぶつけてみてはいかがでしょう.
最後の講演の野間さんは,今回の岩波DSには書かれていませんが,こちらの本 こちらの本 に執筆されています.今回は,因果推論とは少しずれますが,医学関係のエビデンスを統合する新しい手法である「ネットワークメタアナリシス」を中心にお話しされます.
その他,DS3の執筆者から津川さん,中村さん,加藤さんが来場される予定です.岩波DSの毎号の表紙の絵は特徴があるので,手に取られた方は記憶に残っているかもしれませんが,その原画を書かれた蛯名優子さんにもご来場頂きます.
* *
東大医学部の大きな階段教室でやりますが,これは都心からの交通の便など考えたためで,医学・疫学が専門の方に特化した講演会ではありません.160人入れるということなので,よほどのことがなければ大丈夫と思います.部外者がめった入る機会のない場所ですので,この機会に覗いてみるのはいかがでしょう.
なお,大講堂のそばには解剖標本室があり,大昔,解剖学専攻の優雅な女性に誘われて見学し,トラウマになった思い出があります.現在では厳重に施錠されており,簡単には見せてもらえないようですが,なんだが祟りそうでちょっと怖いです.医学部の学生が普通に講義を受けている場所なので大丈夫なはずですが,医者は特別の厄除けパワーがあるかもしれないし,危険かもしれません.
岩波データサイエンス3巻「因果推論」発売
先週末にようやく岩波データサイエンス3巻が発売になり,少しほっとしています.
サイエンスブログもそろそろ新ネタを投入したいところですが,もう何年もずっと書いている著書(確率統計の入門書)のほうもやらないといけないので,次はまた番外編になりそうです.持ちネタの半分くらいはもう出してしまいましたが,残りの半分はゆっくりと行きます.
サイエンスブログの本題とはちょっとずれるかもしれませんが,今回の特集の「因果推論」の前半は読みやすい内容なので,再度ご紹介します.ツイッターのほうをごらんの方はすでにいっぱい宣伝をしているので,読み飽きていると思いますが,すみません.
表紙はこんな感じ.小さくてハンディな判型です.芥川賞作家の円城塔さんに毎回見開き2ページの小説を書いて頂いています(今回のはブラックというか自虐ネタすぎて笑えます)

中身のほうは目次や特集の前書きがここで無料で読めます(登録不要,PDF) http://www.iwanami.co.jp/.PDFS/02/4/0298530.pdf
こちらが1巻から共通のサポートページトップとなっております.
岩波データサイエンス
* * *
【再掲】前回書いたカジュアル版の解説をこちらに移動しておきます.
「因果推論」というと,なにか難しい特別なもののように思われるかもしれませんが,簡単に言ってしまえば「相関」と「因果関係」は違う,という話です.
たとえば「運動をする人は健康状態が良い」ということから「運動をすれば健康状態が良くなる」とはいえません.すごく体調が悪かったら運動はできないので,その分を差し引いて考えなければならないでしょう.
仮に「お酒を飲む人にはガンが多い」というデータがあっても,それからすぐには「お酒を飲む人を減らしたらガンが減る」とはいえません.たとえば,お酒を沢山飲む人はタバコも吸う傾向があって,ガンの増加はお酒でなくタバコのせいかもしれないのです(実際にはガンの種類によっては過度の飲酒が原因になることがわかっていますが).
では,どうすればよいか,ということも含めて,この分野のさわりをまとめたのがこの巻の特集です.統計の予備知識がちょっとしかない人でも気軽に読める記事も,ある程度勉強された方に役立つ記事も両方入っていますので,幅広く役に立つことを期待しています.