はしか物語(1+2) 病気の振動と絶滅,都市の誕生
今回のシリーズは麻疹(はしか)の話.
修士課程で氷の研究をしたあと,博士課程のはじめくらいに,伝染病のシミュレーションを格子の上で走らせて遊んでいたことがある.和文論文をひとつ書いたのだが,いま読むと何をやっているのかよくわからない内容なので,引用するのはやめておく.セル・オートマトンとかepidemic processとかが流行っていたころで,「物理」のセンスとそうでないものの間でなにか模索していたのだと思う.
それから10年以上たって,自分が成人麻疹に罹ってしまい,危ないところだった.2015年で国内由来のはしかは3年連続でゼロになり「排除宣言」がされた由で,輸入される麻疹はあるにしても,発症数は激減している.いまや成人麻疹は貴重な体験かもしれないので,最後の回はその話を書くことにしよう.
(1+2),3【改訂版】,(4+5)の全3回にまとめ直しました.
振動したり絶滅したり
伝染病の流行には振動がみられることがある.病気がどんどん広がって行くと,いちど罹って回復して免疫を持つ人が増える.あるいは人々が死んでしまって感染できる相手がいなくなる.人間にとっては大きな違いだが,病原体にとってはどっちでも同じことで,火事が燃えるものがなくなって自然に消えるような現象(絶滅,extinction)が起きる.
ここで,新しい人が全然加わらなければ,絶滅しかないわけだが,生まれてきたり転入してくる人が一定以上いれば,復活もありうる.病気が下火になるが,ゼロではない状態がしばらく続くと,その間に感染可能な人の数が増えて,あるところから,また「どーん」と流行するわけである.これを繰り返せば振動になる.もちろん振動しているうちに運悪く絶滅してしまう場合もある.
こう書くと,プログラミング好きの人はさっそくモデルを作って試したくなるだろう.確率モデルの詳細は後で示すとして,とりあえず,結果だけ見せよう.
以下の図の横軸は時間(シミュレーションのステップ数),縦軸はその時点で病気に罹っている人の数(あとのプログラムではx[2])である.3つの図は,同じパラメータで,乱数だけ変えたものに対応する.乱数を使ったモデルなので,他の条件が同じでも偶然によって差が生じる点に注意されたい.
まず,そこそこ振動してから絶滅する例.
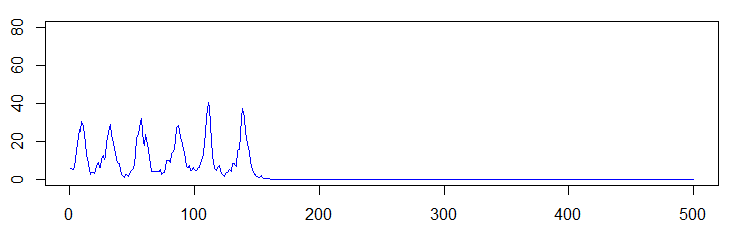
こんどは長持ちの例.
と思うと,広がらずに,あっという間に終わることもある.
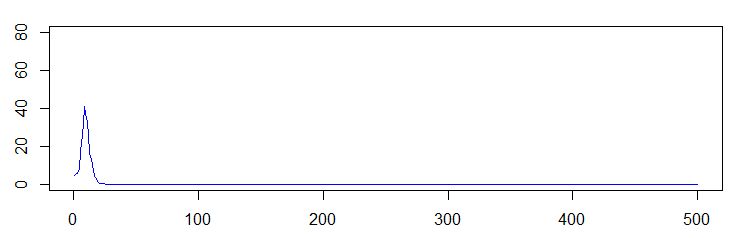
ちょうど微妙なパラメータの値を選んでいるせいもあるが,想像するよりも偶然の余地が大きい.うんと減ってしまったところで,1人でも患者が残っているかどうかで患者数が回復するかどうか決まるわけで,そこで偶然が入るわけである.
Critical Community Size
都市のサイズが小さいと都市内部の出生数が少ないので,すぐに絶滅してしまうが,実際には「外部」があるので,そこからまた病気が侵入する.その結果,見た目は似たような振動が起きるが,よくみると途中で内部の患者がゼロになる期間がある点が違う,
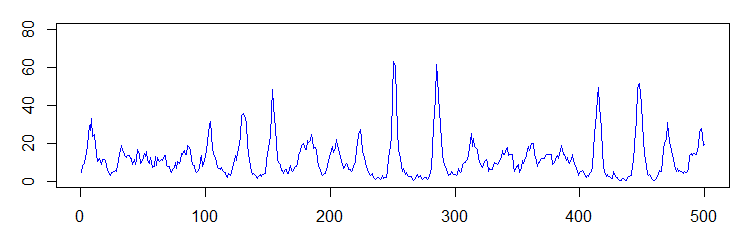
シミュレーションだとこんな感じだ.こんどは「外部」のあるモデルになっているので,絶滅してもいつかは復活できる.ピークが妙に等間隔に見えるのは,絶滅後しばらくは免疫された人が多くて侵入できないためである.刺激されても反応できない「不応期」みたいなものがあるわけだ.
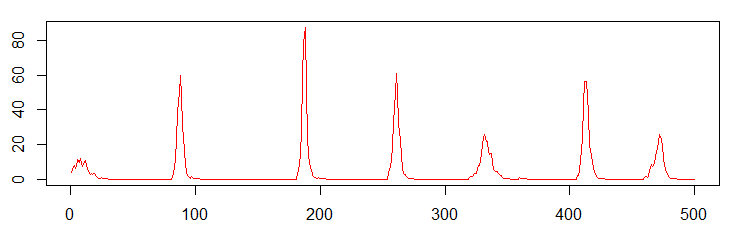
伝染病が維持できる限界の都市のサイズはいろいろなパラメータによって変わるが,これをCritical Community Sizeと呼ぶ.「臨界サイズ」といっても,本当にそこで定性的な性質が変わるわけではなく,目安のようなものである.Critical Community Size以上でも一定の時間内に絶滅する確率は有限だが,非常に小さくなり,実際上はゼロとみなされる.
都市といっても「内と外」がそんなに厳密に分かれているとは限らないので,よりきれいなデータを求めて離島での流行の様子を調べた研究もある(あとの文献参照).小さい島だと外部からの再侵入によって流行が起きるが,大き目の島なら自分の中で病気が維持されることになる.
都市の出現と麻疹のウィルスの進化
いまの話から「人類が都市を形成する以前にはどうだったのだろう」という疑問を思いついた人がいる.
麻疹の場合には Critical Community Size はかなり大きいので,人類のあけぼのの時代には,そんな大きい都市(というか人間が固まって住んでいる場所)はどこにもなかったと考えられる.どこにもないのだから,外部からもらうというわけにもいかないわけで,麻疹ウイルスは自分で自分の首をしめて自滅してしまうほかない.
動物からうつる,と思うかもしれないが,少なくとも現在の麻疹は人間しか罹らない.天然痘と同じで,だからこそワクチンで撲滅しようという話が現実味を持つわけである.
これは麻疹が存在するという事実と矛盾するようであるが,実は,麻疹のウイルスが動物(おそらく牛)から人間に宿主を変えたのはかなり新しく,「都市」が誕生したあとになってからだと考えられている.それまでの間は,麻疹ウィルスはたとえ「種の壁」を超えても,その先ずっと人間の間ではやり続けることはできなかったということになる.
病気にかかるのは個々の人間なのだが,ある意味では「都市」というシステムが病むわけである.
こういう話を聞くと,こんどはウィルスの進化のシミュレーションが作りたくなるが,結局「ウィルスが変異したときに抗原としての重なり(抗体の交差)がどの程度あるのか」といったパラメータの決め方でどういう答えでも出そうで,面白い結果を出すのは難しそうな気がする.
麻疹は猛毒だった?
ところで,麻疹という病気を全く知らない土地にはじめてウイルスが侵入すると,大変な威力を示して,住民の大半が死んでしまう,という話がある.たとえば,フィジー諸島に麻疹が侵入したときは大変に高い死亡率であった伝えられているし,他でもそういう例がある.
「免疫がなかったから」というのは大流行の理由にはなるが,死亡率はまた別の問題である.ひとつ可能性のある説明は,われわれは麻疹に対抗できるように進化したが,麻疹のない土地に住んでいる人たちは抵抗力がないままだった,というものだ.
ここで「進化」と簡単にいったが,その実態は「われわれの先祖のほとんどは麻疹に罹って死んだが,ごく少数のミュータントが恐ろしい病気にも耐えられた.我々はすべてこのミュータントの子孫である」という意味である.
想像してみよう.
猛烈な感染力を示す謎の病気で倒れる人たち.この病気は生体を防御するリンパ球自体を狙って感染し,胸腺などのリンパ組織を破壊してしまうという不気味な性質を持っている.いったん解熱したように見えても,再び熱が上がり,恐ろしい真っ赤な発疹が出て死んでゆく.あっという間にどこもかしこも病人と死体の山となり,人類の希望はついえたかのように思われた.そのとき,ウイルスに打ち勝って回復する特異体質の人がごく少数存在することがわかる.生き延びたミュータントたちが文明を再建したのである.
自分がそういうすごいミュータントの子孫だと思うと,誇らしいような怖ろしいような,ちょっと変な気持ちになる*1,
もっとも,今回改めて調べてみると,これにはほかの可能性もあるようである.グリーンランドにはじめて麻疹が侵入したときは大流行になったが,死亡率はそれほど高くなかったともいう.数十パーセントというような死亡率は,大流行で社会のインフラが崩壊するとか,何かほかの副次的な現象によるのかもしれない.
また,ヨーロッパでは麻疹の死亡率がある時代から下がった,という話もある.この場合は,麻疹ウイルスに対抗できる人間が選択されたというより,ウイルスのほうが変化した,あるいは,栄養状態その他によって人間の生き延びる力が増えた,ということが重要なのかもしれない *2
「都市の発生」には麻疹への耐性が必要だった?
前回紹介した話は「麻疹ウィルスの誕生が都市の形成を前提条件にして可能になった」というものである.
しかし,逆方向の話もありうるのではないか*3.まず,麻疹ウィルスの毒性が(当時の人類に対して相対的に)いまよりずっと強かったと仮定する.また,牛から人間への「種の壁の突破」が比較的容易で,歴史の中で何回も繰り返し起きたとしよう.そういう状況だと,逆に「麻疹に対する抵抗性が進化してはじめて都市というものが可能になった」ということはないだろうか.
また妄想.
古代のどこかの地方で,町が栄えて,都市の原型が形成され,さらに発展して行く.人々は明日の繁栄を疑わないが,少数の古老だけが「こんな賑わいには罰があたる.伝説の赤い悪魔がきっと来る」と不吉な預言をする.・・・ そこでお約束の病気の出現である.無残な赤い発疹.機能しない免疫系.生まれたばかりの都市は無数の墓を残して廃墟になる.人々の記憶こそ毎度曖昧であるが,こうしたことが100年,200年の間隔をおいて繰り返される.バベルの塔の倒壊とは実は麻疹のことだったのだ(嘘).
・・しかし,ついにウィルスに打ち勝つミュータントが赤い悪魔に勝つ日が(さっきの妄想に続く),という筋書きは面白いと思うのだが,やっぱり無理だろうか.
(おまけ)シミュレーション・モデル
シミュレーションのコード
さっきの図を作るのに用いた確率モデルを説明しよう.
いろいろなモデルが考えられるが,以下では離散時間の簡単なモデルを考える*4.また,ここでは「都市」の中にできる感染者の塊(空間パターン)の効果は考えない(いわゆる平均場モデル).「遠くにいる人にはうつらないのではないか」という疑問もあるが,その分はうつりやすさを決めるパラメータ(下記ではlam)の値が小さくなることで表わせるとする.
数式で書くより,時間発展の手続きをプログラムで説明したほうが早そうだ.いつものようにR言語で書くことにすると,コードの全体はこんな感じになる.
xinit=c(75,3) lam=0.01 nu=6 alpha=0.5 theta=0 col=4 k.repeat=1 n.length=500 x.record=array(0,dim=c(n.length,k.repeat)) for (k in c(1:k.repeat)){ x=xinit for (n in c(1:n.length)){ newseed=rpois(1,theta) new=rpois(1,lam*x[1]*(x[2]+newseed)) add=rpois(1,nu) x[1]=x[1]+add-new x[2]=alpha*x[2]+new if(x[1]<0) {print(x);x[1]=0; } if(x[2]<0) {print(x);x[2]=0; } x.record[n,k]=x[2] } } plot(0,0,type="n",xlim=c(1,n.length),ylim=c(0,max(x.record[])),xlab="",ylab="") for(k in c(1:k.repeat)) lines(1:n.length,x.record[,k],col=col)
以下,各ステップを大まかに説明するが,別にこれが標準的なモデルというわけではなく,とりあえずそれらしく動いて遊べるという程度の話である,
モデルのプログラムの説明
各時点でのシステムの状態をきめる変数
x[1] 感染者の数. x[2] 感受性のある人(免疫を持たない人)の数.
x[1]とx[2]を1ステップ時間発展させる手続きは以下の4つで決まる.
1.外部からの感染者の流入
newseed=rpois(1,theta)
ここでは,各時点の外部からの感染者の流入newseedが期待値theta(定数)のポアソン分布に従うと仮定する.rpoisというのはR言語の関数で,期待値を与えてポアソン分布にしたがう乱数を発生させるものである.期待値thetaをゼロにおけば「外部からの感染者の流入なし」のモデルになる.
2.感染
new=rpois(1,lam*x[1]*(x[2]+newseed))
「(内部の感染者数x[2]と外部からの感染者数newseedの和)=感染源の数」と考えて,「感染源の数×感受性のある人の数x[1]」に比例して,新たに起きる感染の数の期待値が定まるとした.それを式で書いたのがlam*x[1]*(x[2]+newseed)である.lamは比例定数.そして,その期待値で定まるポアソン分布で新たな感染者の数newを発生させる*5.
3.回復→免疫獲得(または死亡)
x[2]=alpha*x[2]+new
感染・発病した人は一定割合で回復するとしたのがalpha*x[2]の部分である.alpha=0.5なら各ステップで半分が回復する.それに新たに感染した数newを加えたのが次のx[2]になる.ここは結構アヤシイ*6.なお回復すると「免疫のある人の数」が増えるが,それは計算に直接必要がないので変数にはしていない.
4.出生(または外部からの免疫を持たない人間の流入)
add=rpois(1,nu)
x[1]=x[1]+add-new
期待値nu(定数)のポアソン分布で新しく生まれた人の数addを発生させるのが最初の式.現在のx[1]にaddを加えて,新たに感染した数newを引いたのが次のx[1]になるというのが2番目の式.
かっこわるいけど
このやり方では,離散時間近似のため,差し引いたあとの人数がマイナスになることがあるが,その場合は強引にゼロにしている,
if(x[1]<0) {print(x);x[1]=0; }
if(x[2]<0) {print(x);x[2]=0; }
すべてがポアソン過程と仮定すれば,連続時間のシミュレーションは標準的なテクニックで可能だが,たとえば病気からの回復がポアソン分布で起きるとは思えないので,必ずしもリアルとはいえないだろう.
完全にリアルにするには個人ごとに状態を設定するのが一番だが,10000人いれば10000の個体(エージェント)を動かすシミュレーションをすることになり,なかなか大変である.実際にスパコンや京コンピューターでそうしたモデルを実装している研究もある.
プログラムの説明の補足
- 乱数のseedは指定していないので毎回出る絵が変わる
- 青い線のグラフを描いたパラメータ.
- lam=0.01
- nu=6
- alpha=0.5
- theta=0
- 外部からの流入で感染者が維持されている状態(赤い線のグラフ)では以下を変更.
- nu=2
- theta=0.05
- x[1]とx[2]の初期値 xinit=c(75,3)
- 時系列の長さ n.length=500
- 全体の繰り返し数 k.repeat=1
- プロットの色 col=4
歴史とか文献とか
ウェブで読める以下の解説は麻疹について包括的に扱っていて大変興味深い(PDF)
http://www.eiken.co.jp/modern_media/backnumber/pdf/MM1007_03.pdf
国立感染症研究所の解説(旧ウェブ,やや古い情報)主に病気としての麻疹についてのまとめ.
IDSC 感染症情報センター
確か自分はこの記事を読んで興味を持ったような気がする.島嶼の麻疹流行の話.
クリフ・ハゲット 「はしかはどのように拡がるか」 日経サイエンス1984年7月号
島嶼の麻疹流行については60年代のこの論文が有名.都市についての話もこれがオリジナルではないかと思う.
Measles endemicity in insular populations: Critical community size and its evolutionary implication
Critical Community Sizeについては,バートレットやケンドールといった昔の大御所の50年代の研究がある.この際勉強してみようかと思ったが,確率過程は得意でないのと,ひたすら読みにくいため沈没.いちばんの基本となる「出生死滅過程」については解析的な取り扱いがフェラーの確率論の本にある.
バートレットも解析的な扱いの限界は理解しており,同じマンチェスター大学でやっていた初期の電子計算機プロジェクトでシミュレーションを走らせている.その話は書いていないが,計算機プロジェクトの話はウィキペディアにある.
Manchester computers - Wikipedia, the free encyclopedia
最後に割合新しいフリーアクセスの論文(モデルのパラメータのデータからの推定がメイン)をメモしておく.
A stochastic model for extinction and recurrence of epidemics: estimation and inference for measles outbreaks
*1:まあこれは「すべての人は無数の精子の戦いに勝利して生まれてきた」というのとあんまり変わらないかもしれないが.
*2:この節の執筆にあたっては,「麻疹,フィジー」で検索すると上位でヒットする以下の文書の情報を一部参考にした.https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0ahUKEwjdu9KG-afOAhXHKZQKHYd6CnkQFgg0MAM&url=http%3A%2F%2Fwww.tm.nagasaki-u.ac.jp%2Fnewrect%2Fjapanese%2Finfectious%2581%2595civilization%2Fprologue.doc&usg=AFQjCNEyWHpOCRcJcSj_8ePE3-ldHOAf5w&sig2=-vYXtMO7-lof9iMrRBK8Iw おそらくこのサイトを運営されている方の訳書・著書のいずれかの一部ではないかと思われるが確認できていない. 長崎大学 熱帯医学研究所 国際保健学分野
*3:こちらのほうの話は,自分で思いついたのか,どこかで聞いたのか忘れてしまった.
*4:パラメータや都市サイズは麻疹の現実的な値には合わせていない.また潜伏期は入っていない.
*5:感染者の数についてポアソン分布でなく逆2項分布を勧める文献もある.
*6:文献には1ステップで全部治ってしまうとする(というか,発症から治るまでの時間を1ステップに対応させる)やり方が出ていたので試したが,なぜかそれだとうまく動かなかった(パラメータが悪い?)