個別性を選ぶということ ー プリーモ・レーヴィとオリヴァー・サックス

プリーモ・レーヴィと「周期律」

プリーモ・レーヴィの「周期律」が本棚に見当たらない。どこにやったのか憶えていないが，アマゾンで調べたら，もう新本は買えないみたいだ。

「周期律」は大変風変わりな短編小説集である。作者は本職の化学者で、各作品ごとにある元素がテーマになっているのだが、その内容がマニアックすぎるのだ。そういうと、軽い筆致の読み物とか、あるいはSFとかを想像するかもしれないが、全くそうでないところがすごい。

プリーモ・レーヴィは収容所経験のあるユダヤ人作家で，この短編集にも，ナチ時代の陰鬱な空のもとで日常を送る人々の心の綾を描くような作品が多い。一口にいえば地味で重厚な作風なのだ。それと絡んでくるのが専門的な化学の話なので、その組み合わせが独特の世界を作っている。

個々の作品のあらすじが簡潔にまとめられているサイトを見つけたので、リンクしておく。blogs.yahoo.co.jp

小説「カリウム」

以下では「カリウム」という短編を少し詳しく紹介しよう。これから読む人もいると思うが、ネタバレしたら興味がなくなるような作風ではないので、あまり問題ないかと思う。

「カリウム」の舞台はナチス時代の大学である。繊細な描写が続くが、そこを全部省いて要点だけにすると、化学を学んだ若者が、たまたま理論物理の若い先生のところに移って、先生カッコいいし物理に変わろうかな、と心が揺らぐ話ということになる。

それが、ある事件をきっかけに、化学者としての自分に目覚める、という結末だが、渋いのはその事件の内容だ。金属ナトリウムの代わりに金属カリウムを使って実験したら爆発しちゃった、という話なのだ。

爆発したことによって、自分の生きるべき世界は、ナトリウムとカリウムが等価であるような普遍志向の世界ではなく、その違いがリアルであるような実験化学の世界だ、という悟りに達する。それがとてもシリアスに重厚に描かれている。

医学や生物であれば、体内でのナトリウムイオンとカリウムイオンの働きがまったく違うのは当たり前で、それでは話が成り立たない。ここでは、有機化学の実験（たぶん脱水の目的）で，両方ともアルカリ金属で周期表でも1行違いの上と下だし、一見すると平気なように思えるのが、実はぜんぜん大丈夫でなかった、というのがポイントである。

「周期律」は基本的に私小説集で、創作も実体験もあるそうだが，「普遍に惹かれつつも個別を選んだ」のは作者の実体験だろう。自分は逆に、個別性に惹かれながら普遍を選んだ人間なので、この話には何となく心惹かれるものがある。

タングステンおじさん

先ごろなくなったオリヴァー・サックスは、脳科学や医学に関する読み物で有名だが、少年時代は化学マニアで、将来の化学者を夢見ていたらしい。その時代のことを書いた本が「タングステンおじさん」で、彼の著作の中でも異色の作品となっている。

www.amazon.co.jp

アルカリ金属の話もあって、素人はⅠ族はみんな銀色だと思っているだろうが、実はセシウムだけは表面の酸化皮膜の関係で微妙に金色を帯びている、という記述が印象的だった。放射性でないセシウムが話題になることは滅多にないし、ひとつ上のルビジウムも同様だと思う。

この本の結末というか、最後に著者が化学への興味を失って医師の道を選ぶところがまた興味深い。著者は量子力学の話を聞いて、自分の愛した化学の時代は終わったと感じたらしい。実際にはそんなことはないと思うのだが、彼はそう感じたようだ。そういう時代の人だったのか、と思うと同時に、彼もまた個別を愛した人だったのだと思う。そして、そこの注釈には、もちろんプリーモ・レーヴィの「カリウム」が引用されているのである。

今日では考えにくいかもしれないが、化学は物理学の及ばない一段深い世界とされてきた。そこに若い物理学者たちが無遠慮に「普遍」としての量子力学を持ち込んで解き明かしてゆく。基本的に自分はそれをカッコいいと思う側の人間だと思う。

それにも関わらず、自分の中には個別を愛する面があって、それが今の仕事につながっているのかもしれない。

（おまけ）アルカリ金属を水に入れてみる動画

Youtubeをみると「いろんなアルカリ金属を水に投げ込んで比較する」という動画がいくつもあって面白い。リチウム→ナトリウム→カリウム→ルビジウム→セシウムと原子番号が大きくなるほど反応性が高くなるというのは化学のテキストに出ているが，実際にルビジウムやセシウムでやってみる機会は滅多にないだろう（それに，ナトリウムだって危険だが，こいつらは実際マジで危ない）。派手なのと真面目なのと両方の例を貼っておく。

www.youtube.com

www.youtube.com

なお，セシウムといっても，ここで出てくるのは放射線を出す同位体ではないし，この実験と放射能は全然関係ないので念のため。

ワトソン君よりアントン君 － 揺らぐタンパク像

ワトソン君よりアントン君

「アントン」の話を初めて聞いたときには，これはもう世間で有名なもので，自分は話題に出遅れているのだと思った．ところが科学や技術に興味がありそうな人に話してみると，意外とみんな知らない．その代わりに話題に出てくるのは，なんとなく響きの似た「ワトソン」のほうである．ワトソンとは何か聞いてみると，ＩＢＭの作った人工知能だそうだ．そんなの面白くないじゃん！

ということで，コンピュータ関係では最近イチ押しのアントン君なのだが，その正体はタンパク質の分子シミュレーション専用機Antonである．特徴は比較的小さいサイズのタンパク質に対象を絞った代わりに，画期的な長時間，現実の時間にしてミリ秒のオーダーのシミュレーションを実現したことだ．ミリ？ 千分の一秒？　たったそれだけ？ と思うかもしれないが，それが業界的にどのくらいすごいかは，あとのほうで説明する．

アントン君については，科学以外の話題もある．この高価な機械は，運営している組織も含めて，大金持ちの個人が私財で作ったものなのだ．その億万長者の名前はDavid Shawという．もともとコンピューターサイエンスの研究者を目指していたのが，途中で民間に移りファイナンスの分野で成功，King Quantと呼ばれて全米ランクに入るようなお金持ちになって，中年から科学に復帰．巨万の富で夢のスーパーコンピュータを作ったのだそうだ． お前はサンダーバードかアイアンマンか．

公平のためにいうと，日本でもMD-GRAPEなど早くから分子シミュレーション専用機が研究されてきたし，汎用の京コンピューターも大きな分子については有力である．とりあえずアントンから始めたのは，専門家がその衝撃を認めていることもあるが，私が長年見たかったあるものを見せてくれたということが理由だ．その話もあとでしよう．

さて，以下では，しばらくアントン君やシミュレーションの話から離れて，なぜタンパク質に興味が持たれ，巨万の富を費やして専用のスーパーコンピューターが建造されるほど注目を浴びるのか，という話をイチからしてみよう．前にプリオンの話を書いたときに前提としたことも，ここで少しだけ説明する．

「お肉」からの出発

まずは，うんと基本的な話から．これ大事だから，とくに生物系の読者はよく聞いてほしいのだが，ごく一般の人に「タンパク質」と言ったら何を考えると思う？　試してみた．

答えは「お肉」．

すげーインパクトだ．科学も技術も一撃で葬り去る威力がある．

そこであわてて説明すると，タンパク質は確かに体重の多くを占める筋肉の構成成分であるが，それだけでなく，体内の化学反応の大多数を触媒として取り仕切っているという点が重要だ．われわれはいろいろな物質を分解したり合成したり変換したりして生きているが，これらはタンパク質の働きなしにはありえない．人間の体という工場の基本部品なのである．

そのほか，呼吸をするときに酸素を運ぶヘモグロビンもタンパク質がベースだし，「お肉」の成分のアクチンとかミオシンも「動く部品」としてのタンパク質の一例である．少し見かけの違うものとしては，爪や髪の毛もタンパク質でできている．こういう「堅くて丈夫」なタンパク質があることは，「プリオン病のもと」が「お肉の成分」と違って簡単には分解されない，ということを納得させてくれる．

ＤＮＡの遺伝情報からＲＮＡを介してまず読みだされるのは，タンパク質を作るアミノ酸の並びだということも，タンパク質が生命の基本だということを示している．ＲＮＡの断片それ自身が関与する場合を除いて，ＤＮＡの情報はいったんタンパク質に翻訳されて働くわけである．植物の体は概して多糖類を多用して組み立てられていて，普通はタンパク質でできた「筋肉」はない．野菜が歩いたら怖いぞ．しかし「最初はタンパクを介してＤＮＡの情報が取り出される」という仕組みは動物でも植物でも同じで，体内の化学反応を仕切るのがタンパク質であることも同じだ．

ここまでをまとめると，最初の一歩は

「お肉」から「生物の基本部品」へ

ということになる．

タンパクの折りたたみとは？

次の一歩は「折りたたみ」(folding)の話だ．

大雑把にいうと，タンパク質の分子はどれも２０種類のアミノ酸が鎖のように並んでできている．多様な役割を果たすタンパク質の基本形はすべて同じなわけだ．その並び順のもとはＤＮＡに書かれていて，ＲＮＡに転写されるときなどに多少とも編集されて，アミノ酸の並びに変換される．　

問題はそのあとである．タンパク質が多様な役割を果たすのは，アミノ酸でできた鎖が折りたたまれていろいろ複雑な形状になるのがミソである．たとえばこんなふうに．

いやこれは巻き尺だったわ．

ちゃんとした絵の入った本職の人の解説を引用しておこう： タンパク質の話（５）

それはともかく，問題は，複雑な形状にどうやって折りたたまれるかである．

答えは「勝手にくるくる巻いて必要な形になる」

実際には，タンパク質の分子がある程度以上に大きくなると「介添人」みたいなタンパク質分子が必要になったりもするらしいが，基本は「引っかかったり絡んだりせずに自力で」なのである．

原理はまったく違うが，形状記憶合金というのに似ているかもしれない．形状記憶合金はあっためるともとの形に戻ったりするが，タンパク質の場合は，いったんターゲットの形状になってから，温度を上げてやると，ほどけて，温度を下げるとまた自動的にもとの形に戻る，というのが実験的に観察されている．

いうまでもなく，これは面白いので，多くの人が長年にわたって研究している．まず，どうやったら，こんなにうまくいくのか，ということが問題になる．神様が作ったのでなければ，生物進化の結果，ということになるが，それだけでなく，うまく折りたたまれるための設計原理みたいなものが知りたいわけである．

また「アミノ酸の配列を与えたときに，それが折りたたまれてどんな形になるか予測する」という問題もあって，定期的にコンテストも行われている．参加者には，まだ実験で折りたたみが調べられていない配列が次々に送られてきて，予測結果を送り返すと，そのあとで実験が行われて比較される，という仕組みである．CASP - Wikipedia, the free encyclopedia． 既知の配列に似たものについては．機械学習や統計科学の手段を用いてかなり予言できるが，全く違うものについては大変難しいそうだ．

この「誰も手伝わなくても自然にうまく折りたたまれる」というのは，どの程度一般的な知識なのだろうか．かなり多くの人が知っているように思われる反面，意外なところで，意外な質問をする人がいる．以前，物理学会のセッションで「鎖を端から作ることが本質的」と信じている人が質問していて，講演者が困っているのを見たことがある．

とりあえず，このあたりまでが，少し興味のある人の平均的知識かもしれない．要約すると

「機械を作るように部品を順番に組み合わせる」から 「放っておくと自律的に形ができる」へ

ということになる．

「最適化」から揺らぐタンパク質像へ

さて，これから先が面白い．

「タンパク質の折りたたみ」というと，カッチリと決まった形に折りたたむ，というイメージが強いだろう．もちろん「有限温度」の世界だから，どんな分子でも平衡の位置のまわりで揺らいでいるが，基本的な形は決まってしまっていて，そのまわりで少しふらふらしている，そんな感じで考えている人が多いのではないか．これを情報科学や計算機科学の言葉でいえば，タンパク質の折りたたみとは，エネルギー最小の状態を求める「最適化問題」だということになる．

しかし，ここ１０年か２０年の間に，そういう四角四面の「折りたたみ」のイメージはしだいに崩れてきている．実際に生体内にあるタンパク質は，もっと自由に揺らいで変形しながら存在している場合も多いらしいのだ．ひとつのタンパク質の中にもキチンと折りたたまれた部分とはっきりした構造をもたない部分が共存している場合もある．

こうした乱れた構造を含むタンパク質はIDP(intrinsically disordered pritein, 天然変性タンパク質）と呼ばれるが，いまやそれは例外ではなく，生体内のタンパク質の相当部分を占めることがわかってきた．IDPがほかの生体分子に結合するときには，くるくるっと全体もしくは一部が折りたたまれて秩序構造になるのがしばしば見られる．

IDPについての説明（日本語の短いもの， 英語ウィキペディア ）

ほかの生体分子に結合する様子の図　
Figure 1 : Intrinsically unstructured proteins and their functions : Nature Reviews Molecular Cell Biology

乱れた領域の生物学的役割についてはいろいろ議論がされているようだが，とりあえず，単にそういうモノがあるというだけではなく，機能に有用な場合もあるということが大事だろう．そして，IDPやその周辺のタンパク質には，人間の病気に深くかかわっていると考えられるものもある．

たとえば，α-シヌクレイン .　

（図はアルファ-シヌクレイン - Wikipedia より）

これはパーキンソン病や多系統萎縮症に深く関係しているタンパク質だが，全体がはっきりした構造を持たないようなIDPだといわれていた．しかし，生体内では，上の絵にあるような一部だけが乱れた形態で，複数が集まったり，折れ曲がって膜に埋め込まれているらしい．

さらにそれだけでなく，一定の条件のもとでは，この形状は不安定化して，もっと固く折りたたんだ（βストランドの多い）形になってお互いにくっつき合って塊になる．そして，この塊（あるいはその前段階？）が自己触媒的に自己増殖するのが病気の本体らしい．これで，前にブログに書いたプリオンの話にもつながったわけである．

そこで，最後のまとめは

「かっちりと折りたたまれたタンパク質」から「絶えず揺らぎ，さまざまに姿を変えるタンパク質」へ

ということになる．

ゆらゆらしたり，くるくる折りたたんだり，別の形態に変貌してその形態が自己増殖したり，現代のタンパク質像はどんどん面白くなっているのだ．

行ったり来たりが見えた！

最後にまたシミュレーションの話に戻ろう．

２０年くらい前にタンパク質の計算をやっている人に話を聞いたときは，大きな揺らぎに興味があるので，それを表現するためのデータ解析手法（主成分分析や有限混合分布的なモデル）をいろいろ考えているということだった．「シミュレーションで見られる大きな揺らぎ」の実例も見せてもらった．雰囲気的にはこんな感じの図．これは本物ではなくて，ペイントで描いた絵だけど．

２つの軸に「主成分１，主成分２」とあるのは，タンパク質の複雑な形状を統計的手法で構成した２つの量で表現するという意味である．図の平面内の曲線の各点がタンパク質の異なる形状に対応している．

本物のデータの例はこちらの北尾彰朗氏の解説論文（以下「北尾論文」）の図２を参照（登録不要で無料で読める）「統計数理」第49巻第1号要旨

北尾論文の図２の軌跡は小さいタンパク質（ヒト・リゾチーム）についての結果だが，対応する物理的時間は１ナノ秒である．タンパク質のシミュレーションの揺籃期の１９８０年代後半には，たとえば１０ピコ秒とかその程度がやっとだったらしい．ナノはピコの１０００倍だから，少なくとも１００倍くらいの能力にはなったことになる．

しかし，どうもまだ不満である．図から「なんかある状態からある状態に移ったらしい」「途中になにか休み場所みたいなものがあるのかな？」ということはわかる．でも，これ，１回きりだよね．何回も行ったり来たりしないと，様子がよくわからないではないか．たとえば，両端の点はいつも再現されるのか，途中の経路はいつも同じなのか．休み場所は本当にあるのか．行ったり来たりを求む！

そして，時がたって，アントン君の時代になった．こんどはミリ秒である．ピコ秒でナノの１０００倍，ミリはそのまた１０００倍だから，０．１ミリ秒（１００マイクロ秒）としても，１ナノ秒の１０万倍だ．揺籃期から比べると，１０００万倍ということになる．１ミリ秒なら，揺籃期の１億倍である．凄まじい進歩だ．

そして，たとえば，こんなふうな結果が出てきた．

前の模式図とは違い，横軸は時間で，縦軸はタンパク質の空間的拡がりをあらわす量である．

おお，行ったり来たりしているではないか！

上はふたたびペイントで描いたウソ絵なので，本物（FiP35タンパクについての100マイクロ秒の計算2回分の時系列）を見たい人はこちらのFig.2aをどうぞ．
Atomic-Level Characterization of the Structural Dynamics of Proteins
サイエンス誌に登録すると読める（すぐ読めるＰＤＦもネットにあったが合法かどうかわからないのでリンクは控える）

実際は，上のサイエンス論文の結果は，北尾論文のような「複数の（準）安定状態の間の行き来」ではなくて，「折りたたんで戻ってまた折りたたむ」という行ったり来たりで，おそらくずっと難しいのだと思う．単に大きなゆらぎを見るのであれば，アントンよりずっと以前にも行ったり来たりが見えた例もあるかもしれないし，もしかすると折りたたみについても初めてというわけではないのかもしれない．

細かくいうといろいろあるのだろうが，ともかく，とうとう行ったり来たりが見える時代になった，というので単純に感動してしまった．行ったり来たりが好きなのだ．

（おまけ）「統計数理」の特集の紹介

タンパク質などの生体高分子のシミュレーションは高次元の時系列データを大量に生成する．これらのデータから起きていることの様子を知りたい，というのは自然な要求である．また，シミュレーションだけでなく，実際の実験でも，１分子レベルでの時系列データをとることが可能になっており，その解析もまた重要な課題となる．

すでに２００１年の段階で，シミュレーションの解析が重要になるのが明らかだったので，「統計数理」の特集号「地図を描く・風景を眺める」を編集したときに，データ解析の立場からのタンパク質のシミュレーションに関する解説論文を２編入れた．上で紹介した北尾の論文はそのひとつである．特集の全体はここで読める．
「統計数理」第49巻第1号要旨

それから１３年がたって，こんどは生体高分子に絞って「シミュレーションデータの多変量解析」の特集を組んだのが，今年(２０１４年）に発行された，以下の号である．シミュレーションデータの解析以外に，実際の実験データ（１分子計測）の解析の話題や効率よく「大きな揺らぎ」をサンプルするレアイベントサンプリングの手法なども扱っている．
「統計数理」62巻第2号要旨

いずれも登録なしで自由にダウンロードできる．一般向きの解説ではないが，この分野に興味のある人，これから研究しようという方には，日本語では他にないまとまった情報源になるはずである．

「統計数理」は他の号もすべてフリーで，ウェブで見られるので，興味のある方はせひどうぞ．
「統計数理」

気象の話の補足

お仕事のほうの記事がウェブに出ました．

気候変動リスク情報創生プログラム：響き合う人とデータ―統数研プロジェクト：統計数理研究所

取材記事といっても内部で作成した広報資料です．　私は他の３人と違って実行部隊ではないですが，少しだけアイディアを出しました．あとはコミュニケーションの整理役かな．

動的平衡なんて怖くない

動的平衡

福岡伸一の「動的平衡」という本が話題になったのは，もうだいぶ前のような気がする．

「あれ～なんかおかしいなあ，動的平衡って別に生物に限らない筈だよねー」とか思ってるうちにブームになり，「文句いおうかどうしようか」と空気を読んでいるうちに話題から去ってしまった，という方も多いのではないだろうか．

「動的平衡」をウィキペディアで見ると，普通の説明を読むことができるが，べつだん生物に限らないことは明らかである．動的平衡 - Wikipedia

統計物理の観点からすると，動的平衡といっても，熱平衡状態やその近傍で見られるものと「非平衡」のものがあるが，前者は釣り合いの状態にある化学反応ならいつでもみられる．たとえば，生物実験で使う緩衝液の中でも起きているが，そのことから「緩衝液は生きている」などと考える生物学者はいないだろう．

非平衡の動的平衡も生物絡みとは限らないが，「非平衡のシステムとして生物を考える」という立場は以前からあって，動的平衡のような概念を持ち込むことは，その観点からはとくべつ新規なものではないと思う．そうした立場を継承している複雑系や人工生命の人が何かコメントをするだろうと思ったが，あまりそういうのは聞かなかった．

福岡伸一本人が本当に動的平衡が生物のみの特徴と考えているのかどうかは不明で，最初の本*1には「動的平衡として生物を定義する」というようなことが書いてあるが，別の本ではこの解説でも取り上げる水の流れや渦のことも書いている．もともとふわっとした話で捉えどころがない．

それはともかく，動的平衡という概念そのものは，生物以外でも生物でもとても重要である．こんど話題になったときに間違って興奮しないためにも，正しく驚くためにも，ふだんからそういう見方を養うのは大切なことだろう．

・・というわけで，簡単な例をいくつか紹介することにする．

溶解度の謎

液体に他の物質を溶かしていくと，ある濃度は溶けないのが普通である．この現象を「飽和」，もう溶けなくなるまで物質を溶かした溶液を「飽和溶液」という．飽和溶液になるまでに一定量の液体に問題の物質がどれだけ溶けるかというのが「溶解度」である．

この「飽和」という現象が，子ども心にとても不思議だった．自分で考えた説は，水とかの中に溶かしこむ物質の「分子」を受け入れる穴みたいなものがあって，そこがいっぱいになると，もう溶けなくなる，というものである（下の図）．この考えは粘土とか沸石とか，そういうものに分子が吸着する様子と思えば，ある程度アリかもしれないが「硫酸銅やミョウバンや砂糖が水に溶ける」といった溶解一般の説明としては無理そうである．

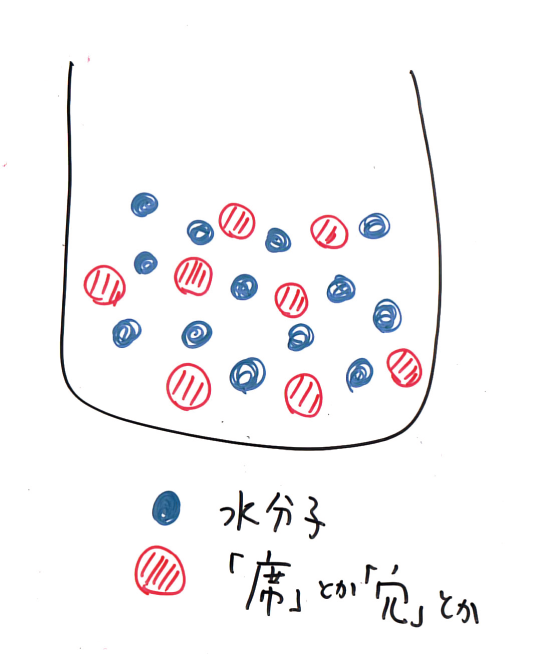
「穴満たし説」しか思いつかなかった自分には，高校の化学の授業で習った「動的平衡」の考え方は衝撃的だった．

分子レベルでは，溶液の濃度が飽和溶液より濃くても薄くても，物質の結晶にくっつく分子もあれば，溶液中に出ていく分子もある．単位時間に出ていく分子の数は，溶液を濃くしても薄くしてもあまり変わらない．これに対して，入ってくるほうは，濃くするほど，単位時間に入ってくる分子の数が多くなる．結果的にどこかで釣り合う点があり，それより濃くなれば結晶の量が増えて溶液は薄くなり，それより薄ければ結晶は溶けて溶液は濃くなる．そして，ちょうど釣り合う点の濃度が飽和濃度である．

図に描くとこんな感じか．

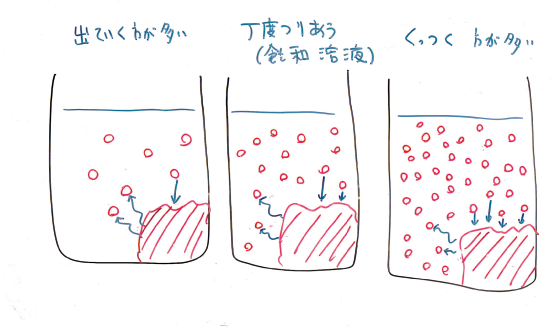
砂糖なら文字通り分子なのが，たとえば硫酸銅だと硫酸イオンと銅イオンになるが，原理は変わらない．面白いのは，見かけ上何も変わらない飽和濃度のときでも，個々の分子やイオンは出たり入ったりしていることで，これが「動的平衡」とよばれる所以である．

「穴に入る」という説明は「穴に入ったり出たり」と修正すれば，動的平衡による説明と両立する．しかし，別に穴など仮定しなくても，もっとずっと一般的に「飽和」という現象を説明できるのが優れたところだ．

ここで，スプーンなんかで結晶をゴリゴリ潰してやると，表面積が増えるが，分子が出ていくほうも入ってくるほうも同じ割合で増える．これは潰すと，溶ける速さ（飽和状態に近づく速さ）は速くなるが，飽和濃度は変わらない，という事実をうまく説明している．結晶を潰すかわりに，スプーンで溶液をかき混ぜても同じだ．

直接に「動的平衡」を証明したければ，たとえば「溶液に溶けている物質の原子の一部を放射性同位体におきかえて，飽和溶液にしばらく浸した結晶の表面から放射線が出るようになる」みたいな実験が必要だろう．

しかし，高校生の私は，一発で，うをーっ，これだ！って感じで納得してしまった．だってすごいじゃないか．こんな説明は全然想像していなかったよ．高校の授業はあまり面白いとはいえなかったので，化学の講義で学んだこの考え方は，自分の高校時代に学校で習ったことのベストワンにしてもいいくらいだ．

ちょっと脱線すると「硫酸銅の飽和溶液に塩化銅は溶けるのか」というようなことが，高校生になった頃には疑問だった．もし，物質ごとの飽和濃度というのが別々にあって，もし各々についての「飽和」というのが独立なことだとすると，硝酸銅，酢酸銅というようにどんどん溶かしてゆけば，銅重なりでいくらでも銅の部分が濃くなるが，それは矛盾だと思えた．そこで，どっちをどっちに入れたのか忘れたが，一方の飽和溶液に一方を入れたら，盛大な沈殿が出てきて，なんか感動した記憶がある．溶解度積とかを習って，そういう現象も普通に理解できるようになったのだが，全然わからない状態で試したのは甘美な思い出になっている*2．

行く川の流れは絶えずして

さて，ここでは平衡と非平衡の区別の説明には立ち入らないが，飽和溶液の話は熱平衡あるいはそれに近いシステムでの動的平衡の例になっている．非平衡というカテゴリーになると，もっと多様な現象が，似たような釣り合いの中で成り立っていることがわかる．

たとえば，台風．台風は，気象衛星からの写真には雲の渦巻きとして写っていて，いかにも「実体」のように見えるし，ニュースでも「北上中」とか「上陸」といかのも実体があるように言う．言うだけではなくて，実際に「実体性」があってなかなか壊れないから，天気予報の役に立つのである．しかし「台風の中身」はどうか．台風を構成している空気の分子や水の分子は絶えず入れ替わっているに違いない．まさに「動的平衡」である．

台風まで大げさにしなくても，小川の流れの中でくるくるまわっている渦も同じく「動的平衡」である．別に渦に限らなくても「流れ」そのものがすでにそうだ．「行く川の流れは絶えずして・・」とはそういう事を言ったのだろう．

少し変わった例としては交通渋滞がある．個々の車は順々に渋滞から脱出して行くのに，「渋滞」そのものは残る．渋滞区間そのものも移動することがあるが，その速さは個々の車の速度とは違う．多くの物理学者が交通渋滞に興味を持って研究しているが，その背景のひとつはこの性質にある．

われわれの社会組織もある意味では動的平衡にある．たとえば，ある学校の「2年生」の中身は毎年変わるが，教員からみれば「2年生」という実体として継続して存在するといえる．翌年になっても中身が変わらないのは，まんがやアニメの学年だけだ．

また「ゼクシィ」や「たまごくらぶ」のような雑誌は「読者が去っていってもその分が常に補給される」ことで成り立っているので「動的平衡雑誌」と呼んでもよいかもしれない*3．

ただ，台風や交通渋滞がいわば自発的に形成されるのに対し「2年生」や「結婚を予定している人の集団」はむしろ外部の条件で設定されるものだから，そこは少し違うかもしれない．同じ動的平衡といっても「ある現象の芽ができると，そこから自然に成長し，自己を維持をする働きがある」かどうかで区別されることになる．そのあたりを考えてきたのが，非平衡のシステムとして生物をとらえるという立場の人たちである．いまの場合に，社会の中で自発的に形成される動的平衡にある集団を見出すことはそんなに難しくないと思う．

定量的な見方も大事

福岡伸一の本でも「生物の体内の物質が入れ替わる速さ」に驚くところから話がはじまっていたと思うが，そういう定量的なことに感動するのはもちろんアリで，とても大事なことである．

体内の物質の入れ替わりの速さのイメージをつかむには，放射性物質の生物学的半減期をみるのがひとつの方法である*4．たとえばここ：実効半減期 - 高精度計算サイト　骨の中のカルシウムが入れ替わるのは50年もかかるらしいので，骨は数年の単位では動的平衡にはないということがわかる．

台風についても「台風が運んできた熱帯の空気で蒸し暑くなる」みたいに思いがちだが，専門の人に聞くと，台風の中の空気の入れ替わる速さはかなり速くて，日本近海にくるころには「熱帯の空気」などはもう含まれていないらしい．

じゃあ，台風が来た前後に，湿っぽくて温かい空気を感じることがあるのはあれは何か，ということになるが，あれは「近場の海から吹く風で湿った空気が流れ込んできている」ということらしい．「いかにもトロピカルな空気だなぁ」と思うのは騙されていたのか．*5．

最後に生物の話に戻って

以上からわかるように「動的平衡によって生物が特徴付けられる」という考えは，「台風や交通渋滞も生物とみなす」という過激な主張をしないかぎり，成り立たない．

逆に「生物が動的平衡の一種である」というのは間違いではなくて，そういう見方をベースにしていろいろ考えていくというのはありだろう．一般に，生物を非線形・非平衡のシステムとみなす，という見方には長い伝統がある．

ただ，現代の分子生物学やゲノム科学は，とても個別的かつ即物的になっているので，そういう「普遍性志向」の方法とはものの見方が水と油の面がある．だからこそ，福岡伸一の本を読んで「これだっ」と思う人が出てくるわけだ．

しかし，そういう考え方が，いつまでも「現代生物学のアンチテーゼ」の役どころにいても，発展性が限られる，というのが過去の教訓のように思われる．むしろ，そういう世界を組み込んだ「ひとつの生物学」が必要なのであって，そこがまさに多くの先覚者が苦労しているところなのだ．

動的平衡とは少しずれるけれど，たとえば縞々の研究からスタートした近藤滋がやろうとしていること，あるいはSTAP細胞に引っかかってしまったS氏がやりたかったことも，大きな流れではそういうことになるかもしれない．普遍と個別，特定の物質に依存しない原理と物質の形をとった原理をどう統合するか．

そういう意味では，動的平衡なんていう考え方には，大人になってから感動するのではなく，早いうちから「普通のこと」として馴れてしまったほうがいい．

*1:「動的平衡」という本は実際は生物に関するエッセイ集のような構成で，動的平衡云々の話が出てくるのは，そのうちのひとつの章だけである．これをタイトルに持ってきた編集者は本を売るという意味では慧眼だったわけだ．

*2:詳しい説明はしないが，溶解度の話を読んで，いまベイズ統計などで使われているMCMC（マルコフ連鎖モンテカルロ法）のアルゴリズムを思い浮かべる人もいるかもしれない．それは正しいアナロジーで，統計物理で開発された手法がデータ解析に持ち込まれた歴史を反映しているのだが，自分の中では「高校のころの感動がいまやっていることにつながっている」といえないことはない．

*3:もっともゼクシィの付録には「妄想用結婚届」がついていたりするそうだから，固定読者も多いのかもしれない．

*4:生物学的半減期と関係付けるというのは筆者のオリジナルではなく，福岡伸一の本のアマゾンでの書評のひとつによる（これ）．なお，この書評には「なぜカルシウムの生物学的半減期は短いのにストロンチウムは長いのか納得がいかない」とあるが，実際はどちらも生物学的半減期は約50年で同じである．ただ，カルシウム45は物理的な半減期が短いのに対し，ストロンチウム90は両方とも長いという点が異なる．

*5:この場合に「熱帯の空気の分子が含まれていない」というのと「湿気の由来は熱帯の空気ではない」というのはうるさくいえば違うかもしれない．まったくの仮定の話だが「熱帯で湿気を吸ったことが最初の原因になって，湿気が湿気を呼び（？），中身は変わったけどずっと湿気がこもっている」というようなことがあれば，どうなるだろうか．

5次方程式の解をぐるぐる動かす

続編です

前回「平方根の日付変更線」の続編である．こんどの話には元ネタがあるが，それは後で紹介する．ただし「ニュートン法で解析接続する」「それをマウスでカチカチ実演する」というあたりはオリジナルである．

こんどは5次方程式

前回は平方根，すなわち，の解をの関数だと思って，複素数の平面上で動かしてみた．このときに「解析接続」に相当するものを「ニュートン法で前の答を初期値と考えて解く」ということだと定義して，の値をマウスでカチカチ入力しながら，解を動かしてみるプログラムも紹介した．

ここでは，平方根の代わりに5次方程式，たとえばの解をの関数として考えて，マウスでカチカチ動かしてみる．対応するソースコードは末尾に添付したが，使い方は「平方根の日付変更線」で説明したのと同じである．

ただし，出力の側のパネルにはのときの方程式の解を○で描いてある．入力側の小さい黒丸は原点を示す．以下の実行結果では，モノクロのほうが入力で，色のついたほうが解である．

さっそく．についてやってみよう．

• まずは原点のまわりをあまり大きく外れないように注意深く回ってみる．すると，無事に5つの根は元に戻った．

• こんどは少し大胆に・・　おお，一対が入れ替わった！

• もっとがーっとやってみる．３つが循環的に入れ替わり，ひとつは元に戻った．

• めちゃめちゃ複雑にしてみたら，なんかすごいことになってる．

という具合で，なかなか楽しい．

別の例

もうひとつ別の5次方程式についてやってみよう．のときの方程式の解はこんどは5角形に並ぶ．

• 小さくまわるとやはり元に戻る．

• こんどは1対が入れ替わった

• えいっとふくらませると

もっと色々できそうである．読者はマウスのカチカチで５つの解を自由に操れるだろうか？

元ネタの本の紹介

5次方程式の解を係数の値を連続的に動かして入れ替える話の元ネタは「ラマヌジャンの遺した関数」（フックス，タバチニコフ著，蟹江訳，岩波書店）である．

『ラマヌジャンの遺した関数』〈本格数学練習帳1〉moreinfo

入れ替わりの背後にある数学的な仕組みは，この本の第5講「5次方程式」に詳しく説明されている*1が，それで終わりではない．この本の面白いところは，そこから発展させて「5次方程式の解を係数から根号と加減乗除であらわす公式」が存在しない理由まで説明してしまっていることである（そういう背景があるので3次でも4次でもなく5次方程式だったわけだ）．

該当する章（長くない）だけを読んでほぼ理解できるので，興味のある方はぜひ手にとって頂きたい．

普通の証明と違うのか？

自分はかなり感動したのだが，そういうと，事情通の人は「それって，普通のガロア理論と群論による証明と違うんですか？」と聞くかもしれない．

いや，あんまり違わないように見える

というのが正直なところかも．最後まで図を念頭に入れて議論しているが，置換群の性質を利用する部分は普通っぽい．結局「置換」をすごく具体的・直観的にやってみせているだけなのかも・・という気もしないではない．

それどころか，普通より劣っているという見方もあるかもしれない．まず，細部まで述べていないので簡単にみえるが，細かい点をきっちり詰めようとしたら，実はかなり煩雑になるのかもしれないという懸念がある．また，普通の議論は，複素数だけでなく，たとえば1+1=0となるような少し風変りな四則のもとで5次方程式を考えた場合にも拡張できる（正標数の場合）．しかし複素数の平面をぐるぐる回る議論はそんな方向に拡張できるようには思えない．

これに対しての弁護としては，まず，この話は，zが不定元であるような普通の「方程式」というより，方程式の定義する代数関数を扱っているような気がする，ということがある．そっちの方向に行く入り口のようにも思えるのだが，その考えが妥当かどうかは，素人すぎてわからない．

しかし，素人の立場でいうと，そういう高度な話よりも「根の置換」ということを，具体的で自然な操作で実際にやってみせてくれるところが，何か想像力を掻き立てるのだと思う．抽象的に置換群を論じるほうが一般性ではまさるにしても，それでは何かピンとこない部分があって，そこが満たされるのである．

その部分をもっと味わいたくて，ニュートン法とか，マウスでカチカチとかを考えてみた，というわけだ．

ソースコード

ほとんど同じだが，5次方程式版のR言語のコードを載せておく．基本的に，互いに違うのはfとdfの定義とzの初期値の設定だけである．使い方は「平方根の日付変更線」の記事と上の実行例を参照．前の記事ではカットペーストと書いたが．直接やると再実行が不便なので，テキストファイルにカットペーストしてsource関数で実行するのが良さそうだ．

バージョン

f=function(z,a)
{
w=z^5-z+a
return(w)
}

df=function(z,a)
{
w=5*z^4-1
return(w)
}

dev.new()
a=0+0i
plot(a,xlim=c(-2,2),ylim=c(-2,2),col=1,pch=20,cex=2)

dev.new()
th=c(1:4)*2*pi/4
z=array(0,dim=5)
z[2:5]=cos(th)+sin(th)*(0+1i)
plot(z,xlim=c(-2,2),ylim=c(-2,2),col=1,cex=3,lwd=3)

zz=z
for(j in 1:1000)
{
  dev.set(dev.prev())
  aa=locator(1)
  points(aa,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=1)
  if(abs(aa$x>2)|abs(aa$y)>2) break
  a=aa$x+aa$y*(0+1i)
  icount=0
  repeat
  {
    zzold=zz
    zz=zz-f(zz,a)/df(zz,a)
    if(sum(abs(zz-zzold))<1.0e-04){print(paste(i," converge")); break}
    if(icount>1000) {print("not converge"); break}
    icount=icount+1 
  }
  dev.set(dev.prev())
  points(zz,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=c(2:6))
}

バージョン

f=function(z,a)
{
w=z^5+a*z-1
return(w)
}

df=function(z,a)
{
w=5*z^4+a
return(w)
}

dev.new()
a=0+0i
plot(a,xlim=c(-2,2),ylim=c(-2,2),col=1,pch=20,cex=2)

dev.new()
th=c(0:4)*2*pi/5
z=cos(th)+sin(th)*(0+1i)
plot(z,xlim=c(-2,2),ylim=c(-2,2),col=1,cex=3,lwd=3)

zz=z
for(j in 1:1000)
{
  dev.set(dev.prev())
  aa=locator(1)
  points(aa,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=1)
  if(abs(aa$x>2)|abs(aa$y)>2) break
  a=aa$x+aa$y*(0+1i)
  icount=0
  repeat
  {
    zzold=zz
    zz=zz-f(zz,a)/df(zz,a)
    if(sum(abs(zz-zzold))<1.0e-04){print(paste(i," converge")); break}
    if(icount>100) {print("not converge"); break}
    icount=icount+1 
  }
  dev.set(dev.prev())
  points(zz,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=c(2:6))
}

（おまけ）「本格数学練習帳」はいわゆる演習書ではないという件

上の「ラマヌジャンの遺した関数」は「本格数学練習帳」というシリーズの1巻なのだが，いわゆる演習書というわけではなくて「具体的で面白い問題を通じて数学を語る」という趣旨だと思われる．シリーズのタイトルをみると，練習問題だけが並んでいる本と誤解されるかもしれないが，それはちょっと違う．練習問題も沢山あるが，基本的には普通に解説していくスタイルの本である．

*1:ヒント．鍵を握るのはが重根を持つの値である．このとき違う色の解が衝突してヤバいことになるが，実はそれらの点をどう回るかが入れ替えを決めている．多項式の重根の条件は，と微分したを連立させたものになるので，それを解いてヤバいの値を求めることができる．

平方根の日付変更線

複素数をなめたらあかんで

複素関数論のテキストを持って歩いていたら，情報系の研究者に「複素数って何に役立つんですか」みたいなことを聞かれた．心外である．２重に間違っているではないか．　

まず，複素数は役に立つ．たとえば，量子力学以降の自然記述では必須だし，これがないと電気関係の技術者もたいへん不便なことになる．次に，何に役立つかとばかり聞くのは立派な数学に対して失礼である．音楽や美術についてはそんなことはいわないのに．

複素数の平方根

複素数の範囲で考えると，実数だけ見ていても思いつかないようなことがいろいろ出てくる．

たとえば，平方根の符号である．

2の平方根にとがあるのは誰でも知っているが，これらは数直線上でゼロの両側の隔離された場所にあり，決して混じったり入れ替わったりはしないように思える．しかし，複素数の範囲で考えると話が違ってくる．複素数の実部を横軸，虚部を縦軸にとった平面を考えて，2からはじめて，原点0のまわりの半径2の円の上を動かしてみよう（下の図の左）．すると，ちょうど一周したときに，平方根は半周しかしないので，はになってしまう（下の図の右）．2周すると元に戻る．

これは「複素数の掛け算では偏角は和に絶対値は積になる」ということの結果である．の平方根は方程式の2つの解のひとつとして定義される．いま，の偏角をとすると，その2乗であるの偏角はだから，を連続的に動かすと，の偏角はのそれの半分の角度だけ変わることになる．が半回転でが90度回り，が１周するとが180度回転して，ちょうど がと入れ替わる．

平方根の日付変更線

このことから，あるについてのをひとつに決めるためには，の値を連続的に変えたときに，どこかでの値が不連続に飛ぶ必要があることがわかる

すなわち「日付変更線」に相当するものが必要になる．これは約束事だから，原理的にはどこに入れてもよい．

たとえば，データサイエンティスト御用達のR言語の複素数型では

>(-2+0.01i)^0.5
[1] 0.003536+1.414218i
> (-2-0.01i)^0.5
[1] 0.003536-1.414218i

となって，実部が負のときに，虚部の符号が変わるところで値が飛ぶ．R言語では下の図の右側で緑色の線を入れたところ（実軸の負の部分）に日付変更線があるのだ．

いくつかの円の上の点の平方根がどうなるかをみると，次のようになる．

ほかの言語では確かめていないが，どれも同じなのだろうか，

もっと複雑な場合は

平方根の場合は簡単に様子がわかったが，もっと複雑な対象について「入力を徐々に動かすと結果がどう動くか」みたいなことを考えるにはどうすればよいか．たとえば「5次方程式のある係数を複素数の平面で動かすとき，方程式の解（これも一般には複素数）はどう動くか」とか．

数学の本をみると，たとえば，べき級数展開（テーラー展開）を利用して，そういう議論がされている．複素数の平面の上のある点の「近く」で収束するべき級数展開を使って「その点での値」から「ちょっと離れた点での値」を計算する．次に，新しい点のまわりで展開し・・みたいなことを繰り返す．いわゆる解析接続である．こうして少しずつずらしていって，ぐるっと回って戻ってくると，関数の値はもとに戻るときもあるし，戻らないときもある．

ここでは，ちょっと違うやり方として，方程式を数値的に解くいちばん簡単な方法であるニュートン法を使う方法を考えてみよう．すなわち

ひとつ前のの値に対して求めたを初期値としたニュートン法によって，新しいの値についての式を解き，新しいの値を求める

とする．各ステップで初期値を介して前の結果が伝わることになる．ベキ級数展開の場合と同じように，これを繰り返してつないでゆく．普通の本で定義されている解析接続との関係をきちんと示すのは簡単でないかもしれないが，実際に試すのはすぐである．

どうせなら，マウスでクリックして動かしてみたい．というので，マウスでクリックした座標で決まるについてのの解を，その前のときの解を初期値にしてニュートン法で計算するプログラムをR言語で書いて，カチカチやって動かしてみた．

黒い点で描いたのがカチカチやって入力したほう，2色の点で描いたのが対応する「ニュートン法による解析接続もどき」の結果である（平方根の初期値がとの場合についての結果を同時並行的に計算している）．図は「1の平方根」の場合の結果である（上に合わせるには2の平方根にすればよかったorz．まあ同じだよね）．ちゃんと半分の角度だけ回っている．

ただ，これは結果の図だけを見てもあんまり面白くない．私はプログラマーとしては超最低レベルなので，普段はソースコードは決して人に見せないのだが，恥を忍んで掲載するので，Rを入れている人はカットペーストして，実際にカチカチやって試してみてほしい．ついでにもっとマシなプログラムができたら教えてほしい．

なに，カチカチやっても別に面白くないって？　うーん，それでは，次回は続編として，5次方程式の解をカチカチやって動かしてみよう．

おまけ

「のかわりにだったらどういう風に日付変更線を入れるか」「変更線の位置によらない性質を直観的に理解するにはどうしたらよいか」という話から，リーマン面が生まれて，三角関数（実数の周期をひとつ持つ）の一般化としての楕円関数（複素数の周期をふたつ持つ）の理論と結びつき，それは20世紀の数学の出発点になった．しかし，その話はきっといろんな人が書いているから，とりあえず，ここではやらない．

ソースコードと使い方

「1の平方根」の場合についてのR言語のコードで，平方根の初期値がとの場合について，並列にの解を計算するようになっている（もっと汎用性があるように書けよ＞自分）．

実行するとふたつのウィンドウが重なって出る．マウスで上のを移動させるともうひとつ下から出てくる（技術力がないので重ならないようにできなかったorz）．最初に上にあるのが,
マウスでクリックしてを入れるウィンドウで，下にあるのが結果が出るほう．どちらも縦軸が虚軸，横軸が実軸．（2次元座標でいえば(1,0)）のあたりをまずクリックして，クリックする点を徐々にずらしていくと，本文中の最後の図のように，１回転→半回転が実演できる．

ニュートン法が100ステップでも収束しないとき（許容誤差は1.0e-04とかに決め打ち）は，そう印刷してあきらめてその値を出すようにしている（そこで終了はしない）．

終了は実部か虚部の絶対値が2より大きい点をクリックすると終わるはず．終わらないうちにウィンドウを消すとRごと落ちてしまうが，落ちると終わるわな（何言ってんだか・・）

f=function(z,a)
{
w=z^2-a
return(w)
}

df=function(z,a)
{
w=2*z
return(w)
}

dev.new()
a=0+0i
plot(a,xlim=c(-2,2),ylim=c(-2,2),col=1,pch=20,cex=2)

dev.new()
th=c(0,pi)
z=cos(th)+sin(th)*(0+1i)
plot(z,xlim=c(-2,2),ylim=c(-2,2),col=1,cex=3,lwd=3)

zz=z
for(j in 1:1000)
{
  dev.set(dev.prev())
  aa=locator(1)
  points(aa,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=1)
  if(abs(aa$x>2)|abs(aa$y)>2) break
  a=aa$x+aa$y*(0+1i)
  icount=0
  repeat
  {
    zzold=zz
    zz=zz-f(zz,a)/df(zz,a)
    if(sum(abs(zz-zzold))<1.0e-04){print(paste(i," converge")); break}
    if(icount>100) {print("not converge"); break}
    icount=icount+1 
  }
  dev.set(dev.prev())
  points(zz,xlim=c(-2,2),ylim=c(-2,2),pch=20,col=c(2:6))
}

ローレンツは気象学者の敵じゃなかったみたいだ

少し前から創生プロジェクトという未来の気候の予測に関する巨大プロジェクトの隅のスミにいる．メンバーはほぼ全員が気象とか防災の専門家だが，試しに統計科学の人もいれてみようということで，私の属している研究所から4人だけはいっている．気象の人たちと話すのははじめてなので，自分でも入門書のたぐいを読んでみた．以下はその感想である．

「スパコンで巨大な数値モデルを計算して予報をしているらしい」というくらいは知っていたが，実際に予報に使われているモデルが地球全体を扱うもの（GCM)だというのはちゃんと認識していなかった．より分解能の高い地域モデルも併用されるが，主力は全球モデルなのだそうだ．原理的には，ヨーロッパや米国の機関の数値計算の結果を使って日本の予報ができることになる．

こうした計算をするには，たとえば60km四方というような網目で全地球を覆う．しかし，地球は丸いので，単純に網目で覆うと，北極や南極のような特異点が避けられない．そこで以前からの方式だと，すべてをものすごく高次の多重極展開（球面調和関数展開）で表現する．これは実座標との変換などで計算負荷が大きいので，正二十面体にまず分割して各面を細分する方式なども開発されているらしい．なかなか大変そうである．

いくつか本を眺めてみて意外だったのは，ローレンツ方程式で有名なローレンツが，リチャードソンと並んで数値予報の礎を作った人と見なされているらしいということだ．「カオス性のおかげで長期の予報は無理だ」と主張したわけだから，きっと嫌われているのだろう，と勝手に思っていたが，むしろ「初期値の違うシミュレーションを多数考えて誤差を推定するアンサンブル予報の考えに導いた」という肯定的な見方をされているらしい．

気象の人たちが確率に対して「わからないということが正しくわかることは重要だ」という正統的な考え方をしているのは興味深い．アンサンブル予報の場合も，たとえば10個の初期値をどれだけ効果的にバラつかせるが重要な研究テーマらしい．単に乱数を加えるのではなく，数日前に遡って乱数を入れ，そこから一定期間ごとにパターンの直交化みたいなことをやりながら互いに離れた10個をえらぶ，ようなことが実際におこなわれている．

こういうやり方では確率分布としての解釈は逆に難しくなってしまうが，それよりも，限られた個数でできるだけバラつかせることを優先している．自らの不確かさをあえて追求する「自虐的な」な考え方は，ある意味では確率ということの真髄をついている気がする．

一般には．高度な確率モデルを駆使する分野の人が自分の結論の不確かさを知りたがっているとは限らない．たとえば，パターン認識や自然言語処理では，目標はひたすら認識率の向上で「不確かさを確かに知る」こと自体に価値を見出す文化は概して薄い．この場合の確率的表現は，むしろアルゴリズムの内部で不確かな情報をやりとりしてうまく統合するのが役割なのだろう．

週間予報のために実際に走っているシミュレーションは，少し前まで51本だったのが，最近では21本になっている．数が減るのはおかしい気がするが，個々の計算に割り当てるリソースを増やしたのだろう．ちなみに「切りのいい数字プラス1本」のプラス1本は何かというと，これは現在の観測値を入れた計算なのであった．

（おまけ）
「地球気」というサイトがあって，色々な天気図などをダウンロードできる．なかでも，週間予報の根拠をA4版1ページにまとめた資料が素人には面白い．アンサンブル予報の台風について「2割はこのあたりにいるが，残りの8割はこちら」などと書いてあると，なんだか親しみがわいてくる．たまには「数値予報では低気圧ができるが（人間の判断で）採用しない」などと書いてあったりもする．

地球気　http://n-kishou.com/ee/

（おまけ２）
これは絶対無理だと思うんだけど，GCMのような数値モデルを使わずに，流行りのDNN（ディープニューラルネット）を使って，パターンを入れたら週間予報が出てくるのが作れたらすごいよね．データはいっぱいあるからやってる人いるかな．全然読まずに石のパターンだけからDNNに囲碁を打たせる，という研究があるんだから，だめもとでやるならありかも．