光の波(上) ― 波から「光線」ができる仕組み,波だから起きる謎の現象
光シリーズの実質最終回ですが,なんか伸びちゃったので上下に分割です.
光と電波は仲間
ときどき思うのだが「光も電波もX線も同じ種類のもの」(電磁波)だというのはどのくらい一般的な知識なのだろうか.日本に住んでいる人の8~9割が普通にそう思っている,という気がする一方で,いや違うのかも,という気もする.実際には,こういうのは「知っている」「知らない」の2択ではなくて「そう言われたらそうかもしれないが,割とどうでもいいと思っている」人たちが多数派なのかもしれない.
自分はというと,小学生のころは科学少年だったから,下のリンクにあるような図がお気に入りで,しょっちゅう眺めては悦に入っていた.こういう図をみると,電磁波の世界は隅々までわかっていて使われているという印象を受ける.しかし,最近よく聞く「テラヘルツ波」はまさにこの図のなかの未探査領域に属する.光と波長の短い電波の中間地帯に十分使いこなせていない「隙間」があったわけだ.世の中はいろんなところで少しずつ進むのだなあ,と思う.
ファイル:EM Spectrum Properties edit ja.svg - Wikipedia
量子力学にもとづく現代的な描像では,光も電波もX線も波の性質と粒子の性質を合わせ持っていて,短波長ほど粒子の性質が前面に出,長波長ほど波の性質が現れやすくなる.しかし,以下では,粒子と波の2重性の話には積極的には触れずに,波の側面に集中しよう.それでも十分面白いと思う.
フェルマーの原理と波
「光が波動である」といったときに,まず最初に問われるのは,光線の挙動,たとえばフェルマーの原理のようなものを波動でどうやって説明するかである.
まず,前の前の記事を復習しておく.「まわりの経路」(下の図の左側の灰色の線)を考えたときに,所要時間がそれらとほとんど変わらないような経路を考える.これは,イメージ的には,下の図の右側の赤い場所に相当する.2点を結ぶ経路のうち,このような経路(所要時間が停留値をとる経路)が実際に光線が進むコースだというのが,フェルマーの原理である.

さて,波で考えるとどうなるか.下の図の左側には停留値でない場合を示した.この場合は,経路をずらすと,ずれの量に比例してどんどん波の山と谷がずれていく.この場合には,問題の経路だけでなく.そのごく近くの経路をまとめて先に足してやると,山と谷が打ち消しあって,振幅はほとんどゼロになってしまう.
一方,下の図の右側には停留値の場合を示した.この場合は,経路をずらしたときの所要時間の変化はゆっくりである(ずれの2乗に比例する).そこで,近い経路をまとめて加えても,激しい打ち消し合いが起きずに済む.

そこで 「自分にごく近い経路を加算しても激しい打ち消し合いが起きないような経路」が有効だと考えると,自然に所要時間の停留値に対応する経路が選ばれることになる*1.これが,波動説によるフェルマーの原理の解釈である.ちょっとはしょりすぎかもしれないが,大筋はこんなところだ.
ファインマン先生による打ち消し合いの解説は,前にリンクした章の最後の部分にある*2.
The Feynman Lectures on Physics Vol. I Ch. 26: Optics: The Principle of Least Time
隠すことで光が集まる !?
波動説でフェルマーの原理が説明できるとすると,次は「波でないと説明できない現象があるか」ということになる.回折とか干渉というのがそういう現象につけられた名前だが,折角なので,少し変わった例を紹介しよう.
波の性質として,山と谷で打ち消し合う,ということがある.そうすると,打ち消し合いに「介入」して,一部を遮ることで,より明るく集中させたりできないだろうか.ピンポン玉や米粒のような古典的な粒子の場合,遮ることで弱くなったり拡散したりはしても,より明るくはならないだろう.したがって,もしそれに成功したとすると,波の性質があることの証明になるかもしれない.
いま「レンズで光を集めたい」という状況で,レンズがまだない状態を考える.この場合,まだ何もないのだから,光線はまっすぐ進むのが当たり前である.フェルマーの原理からいっても,まっすぐ進む経路が唯一の停留値を与える経路だ.波で考えると,ど真ん中をまっすぐ進む経路以外では,隣接の経路との時間差が激しく変化しすぎて打ち消しあう,ということになる.これらは概ね正しいのであるが,そういわずに,まんなかの経路の近くをぐいっとアップしてみると,下の図のようになる.
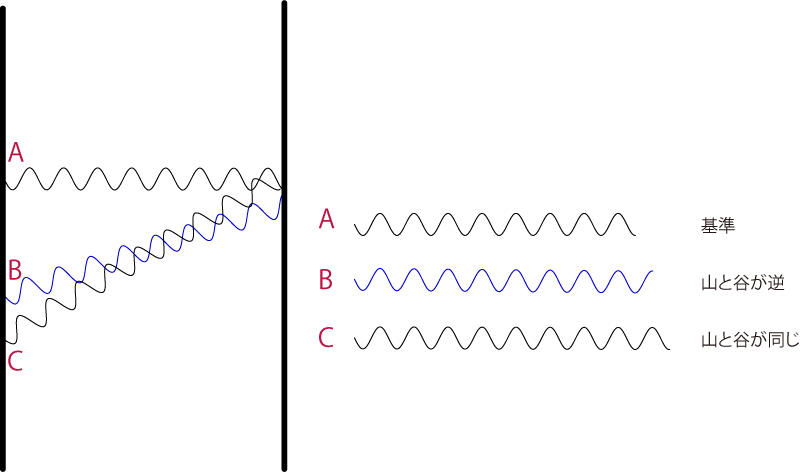
ど真ん中(A)からずれると,光の行く距離がピタゴラスの定理で長くなり.波の山と谷の位置がだんだんずれてきて,あるところまで行くとまったく逆になってしまう(B).もう少し行くと,逆にまた合ってくる(C).さらにずれてくる・・ を繰り返すことになる.面倒なので図に描いていないが,中心から反対側にずらしても同じだ.前にレンズの公式のところでやった計算によると,長さの増え方は中心からの距離の2乗に比例するので,ずれる速さは中心から離れるにしたがって速くなり,合ったり外れたりの周期は短くなる.
真ん中の光にとってみれば,山と谷が合う(経路の長さが波長の整数倍ずれる)波は強め合うことのできる「味方」であり,山と谷が反対になる波は打ち消し合う「敵」だということになる.敵の位置が計算でわかっているのだから,その場所を黒く塗るとかしてブロックしてやったらどうなるだろう.こんな具合にだ.

こうすると,レンズがなくても,あたかもレンズを置いたように,狙った位置に光を集めることができそうな気がする.一部を塗り消しただけで光が集まるのは常識的にいうと奇妙だが,波の説が本当ならそうなるはずだ.
まさかと思う人もいるかもしれないが,実際にそういうものが存在して「フレネルゾーンプレート」(Fresnel zone plate)と呼ばれている.上は断面図なので,実際には中心から遠くなるほど間隔のせまい同心円を交互に黒く塗ることになる.
画像検索の結果はこの通り.
fresnel zone plate - Google 検索
上の断面図をみると「これってヤングの実験じゃん.学校で習ったよ」という人もいると思う.基本的にはそれで正しいのだが,ヤングの実験では「しましま」(干渉縞)が見えるだけで写真はとれないだろう.フレネルゾーンプレートはレンズの代わりに使って写真が撮れるのである.以下のリンク先のサイトに作例がある.
なお「しましま」を見るだけなら,2本の指の間を狭くして,隙間から明るいところを覗く,という方法がある(ファインマンの本に出ている).やってみると,1本か2本かわからないけど,確かに見えるような気がする.
ーーーーーー
(後日補記)
ピンホールカメラといういうのがあって,これは真ん中の穴だけで風景が逆さに写る,というものである.古くから知られていたらしいが,考えてみればこれも光を遮ることで像が見えるわけだ.ただ,これだと光が波であることを考えなくても,光線のレベルで「他の光で分量的に消えてしまわないようにしたから像が見えるようになった」で説明できるだろう.そう考えると,フレネルゾーンプレートの場合も,同心円の幅を変化させたりして,像が消えたり弱まったりするさまを観察しないと,波である証拠としては不十分かもしれない.ピンホールによる逆像の歴史については.たとえば,リンク先のブログ(すごい充実した内容)のトップから少し下のところにある
http://www7b.biglobe.ne.jp/~photojii/SLR/SRL.htm#top
ーーーーーー
ゾーンプレートがレンズになるのなら,もう現実に光を集めたりしなくても,光の山や谷(位相)をセンサーで測っておけば,あとからコンピューターで計算して自由に画像が作れるのでは? と思う人もいるかもしれない.残念ながら,光の波については位相を直接測定するセンサーはないので,それは多分無理である.デジカメのセンサーでも人間の眼でも,信号を2乗した強度を時間平均したものしか測れないのだ.しかし,もっと波長が長い電波について,そういう方式でバーチャルな電波望遠鏡を構成することはかなり以前から行われている.原子時計などを使って正確に観測時刻を測っておけば,地球の反対側のデータと組み合わせて巨大望遠鏡を作ることも可能である.最近の話題としてはこんなのがあった. www.huffingtonpost.jp
こういう方式だと,電波を測定できる場所は全体のうちほんのちょっとで,普通のレンズやゾーンプレートのように「丸い範囲の全体」というのとは全然違う.厳しい条件での画像再構成になるので,ベイズモデルやスパース推定のような新しいデータサイエンスの手法のよい応用対象になっている.
ーーーーーー
ポアソンの斑点(アラゴの斑点)
光が波である証拠として学校で習うのは,計算が簡単な「ヤングの実験」で,歴史的にもそれが先行しているが,発見されたときに衝撃的だったのは「ポアソンの斑点」(Poisson spot, Arago spot)である.
正確な円形の光を通さない板を平行光線に垂直に置くと,当然丸い影ができるのだが,そのど真ん中に明るい点が出現する,というものだ.光を通さない板が光を通したら矛盾だが,これは波が縁を回りこんでいくので,通り抜けるわけではない.
そんなの見たことないぞ. こう書いていても本当とは思いがたいのだが,ウェブを見ると,いろいろ実験例がある.いや確かに光ってますわ.
https://www.kth.se/social/files/55f1b177f276540261b6a04b/arago092015.pdf
ひとつ目のリンク先は緑色のレーザー(たぶんレーザーポインター)と小型天体望遠鏡の組み合わせである.カセグレンとかシュミカセとかマクストフとかいう類の望遠鏡には中心軸上に円形の鏡があるので,これをうまく使っている.ふたつの図のうちひとつはシミュレーションだが,ホンモノのほうもはっきり写っている.もうひとつのリンクは普通の光での検出にチャレンジしている.
斑点に名前がふたつあるのには曰くがある.波動説に基づくフレネルの論文(学位論文ではなく懸賞論文らしい)を審査したポアソンが斑点の存在を導出して「その説が本当だったら,こんなヘンなことになる.ありえへんやろ.やっぱり光は粒子や」と言った.それを聞いたアラゴが実際にやってみたら「やっぱり光ってましたわ」となって,ポアソンびっくり.それで両方の名前がついているのだそうだ.まさに「科学は常識ではない」の良い例だろう.
ポアソンの名前はポアソン分布とかでよく聞くが,アラゴは知らなかった.調べてみると,子午線の測量に行って逮捕されて脱出して海賊に襲われて難破したが無事データを持ち帰ったり,ファラデーより前に電磁気の面白い実験をしたり,オーロラと磁気の関係を指摘したり,大臣になったり,大活躍のすごい人のようだ.
フランソワ・アラゴ - Wikipedia
ポアソンの斑点のできる仕組み
ポアソンの斑点の仕組みはけっこう微妙である.完全な円形ということから,円のふちから中心までは等距離なので,光の波の山と谷はぴったり合う.それで明るくなるのだ,という気がするが,実際は円のふちだけでなく,もっと外から来る波もあるはずである.
ゾーンプレ―トの説明に使ったときの図のように,山と谷が合った部分と合わない部分に帯状に分けてみると,外にいくにしたがって,距離に反比例して帯の幅が狭くなる.だったら,外のほうは「ひとつ置きに符号が変わって打ち消し合いながら,それぞれの帯の寄与自体が距離に反比例して減る」のかと思うと,それは違う.上の図は断面で,本当は円形に分けるので,外に行くほど円周は伸びていくので,(帯の幅)X(円周の長さ)は一定になってしまうのだ.
結局ちゃんと積分しないとわからないわけだが,計算のキモの部分はあとのおまけに示した.
アラゴの斑点,系外惑星観測の大計画を邪魔する
ウェブを眺めていたら,すごい計画を見つけた.太陽系外の惑星を観測するために,宇宙望遠鏡とセットで「遮蔽体」を軌道に乗せる.遮蔽体は望遠鏡の数万キロ前方を飛んで,星の光を遮り,惑星の観測を可能にする.壮大な話なのだが,真ん丸の遮蔽体にすると・・ そう,ど真ん中にアラゴの斑点が出てしまうのだ.下記の論文は線形計画法を使ってスポットが出にくい遮蔽体(たぶん周辺部を半透明にするのだと思う)を設計するという内容のようである.
https://www.princeton.edu/~hcil/papers/rvdbp_PoissonSpotPaper2.pdf
前向きの応用としては,円盤や球の中心を正確に計測するのにも使えるらしい.
以下はおまけ.
(おまけ1)波の打ち消し合いの数学,負符号問題,(ついでにタイムパラドックス)
この解説で述べたような「波の打ち消し合い」に相当する仕組みの解析はここ300年ほどの数学でかなり重要な位置を占めているようで,易しいものから高級なものまで色々調べられている.
1次元版の比較的簡単なものとしては,たとえばこんなのがある.
リーマン・ルベーグの定理(1)
物理や工学のあちこちで出てくる「フレネル積分」というのも発端は光の波の数学である.
高次元での打ち消し合いを一般的にかつ厳密に扱おうとすると,もう筆者の守備範囲外であるが,ヘルマンダ―とか出てきて怖そうだ.
振動積分作用素 - Wikipedia
量子力学のファインマン経路積分になると,素朴に理解するのは容易でも,実時間のまま数学として顕密に扱うのは大変らしい.同じ経路の重みを扱うのでも,正負の符号や複素数が出てきて,大規模な打ち消し合いが主役を演じるので,ウィナー積分とは違って経路の空間の測度は一般には定義できず,ずっと微妙なものになる.
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1723-01.pdf
数学的に厳密な扱いだけでなく,数値的な計算もまた大変である.高次元になってくると,乱数を使ったモンテカルロ法,とくにマルコフ連鎖モンテカルロ法が使いたくなるが,波の打ち消し合いが主役を演じるような量子的な問題への適用はかなり限られてくる.重要な経路を選んだつもりでも,どんどん打ち消し合って効率が上がらないことがしばしば起きる.これを負符号問題というが,そもそも確率とかブラウン運動のような世界と量子力学は根本的に違うので仕方がないともいえる.
ーーーーーー
(おまけのおまけ)
タイムパラドックスも経路積分の打ち消し合いで説明できる!というのがあるそうで,わかりやすい解説がここにある.タイムパラドクスのあれ | phasonの日記 | スラド もちろん教科書に乗るような話ではないと思うが,楽しそうだ.最小作用の原理ならぬ最小矛盾の原理,時間旅行停留性の原理である.ただ,時間的閉曲線のある場合の量子力学が整合的に定義できるのかどうかはよくわからない.リンク先の論文は見ていないが,こんど読んでみよう.
ーーーーーー
(おまけ2)回折理論の系譜(圧縮版)
上で波について計算したやり方は,波の方程式をきちんと扱うのに比べると相当に近似的である.まず,各点から波が出ていくとしたが,これは本当は平面波でなく球面状に広がる波で,強さが距離に反比例する因子がつく.それを入れて17世紀のホイヘンスのレベルになる.ホイヘンスは波が前に進んで後ろにはいかないと述べたが,その正しい表現を取りこんだのが19世紀前半のフレネル,そして波の方程式から正確な表現を求めて,フレネルの結果をその近似として出したのが19世紀後半のキルヒホフ,という位置付けになるらしい.
Kirchhoff's diffraction formula - Wikipedia, the free encyclopedia
「各点から要素的ななにか(いまの場合は波)が出て解はその重ね合わせになる」という考え方の起源は古い.たとえば「地球を細かいかけらに分けて全体の引力を計算する」というようなやり方にもそれは含まれている.しかし,ホイヘンスやフレネルが波について考えたことは,そういう考え方が一般化され発展していく中で重要な役割を担ったと思う.その本質は線形性ということだが,グリーン関数とかインパルス応答とか伝搬関数とか,名前はまちまちでも,そういう考え方は現代の科学や工学のいたるところで使われている.機械学習で使われるカーネル法で「推定結果をデータを代入したカーネルの和で表現する」というのも,その遠い子孫だといえないこともない.
(おまけ3)ポアソンの斑点の計算
以下,や
で書くこともできるが,複素指数関数
を使わないとだんだん我慢会のようになるので,使ってしまうことにする.複素数の答の絶対値が波の強度,位相が波の位相に対応するというのが解釈のルールである.
ざっくりいうと,ど真ん中の光の波を求めるには次のような積分を計算することになる.これになにか未知の複素数の定数がかかっているかもしれないが,その分は遮蔽物なしの場合との比で考えればよいだろう.
ここで,が波の出てくる点の中心からの距離,
が円盤の半径,
が波長とかスクリーンまでの距離とかそういうのが入った実数の定数である.本文で述べたように中心からの距離の2乗で位相がずれるので
の中は
になっている.一方,円周の長さが
に比例するので,積分のほうに
と
が入っている.
下端はいいとして,上端のはどうしたらよいだろうか.実際には,フレネルの理論では含まれているがここでは省略した因子(傾斜因子)の効果がある.また,それ以上に,次回に述べるように,光の波は完璧ではないので,あまり大きくずれると位相がランダムにずれてくる.こうした事情を考えると,うんと外側の寄与に相当する最初の項はゼロと見なしてよさそうである*3.すると,積分は以下のようになる.
この計算結果は以下のように表現できる.
円形の遮蔽物を置いた効果は,中心では位相の変化だけで,絶対値はによらないのである.従って,中心はいつも遮蔽物がないときと同じ明るさになる.これがポアソンの斑点である.